题目内容
(本大题满分18分)本大题共有3个小题,第1小题满分4分,第2小题满6分,第3小题满8分.
已知函数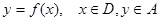 ;
;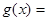
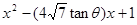 ,
,
(1)当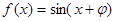 为偶函数时,求
为偶函数时,求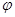 的值。
的值。
(2)当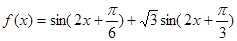 时,
时,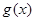 在
在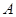 上是单调递增函数,求
上是单调递增函数,求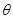 的取值范围。
的取值范围。
(3)当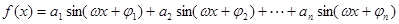 时,(其中
时,(其中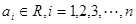 ,
,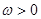 ),若
),若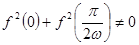 ,且函数
,且函数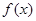 的图像关于点
的图像关于点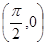 对称,在
对称,在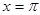 处取得最小值,试探讨
处取得最小值,试探讨 应该满足的条件。
应该满足的条件。
【答案】
(1) ,
, ;(2)
;(2) ,
, ;
;
(3) ,
, 。
。
【解析】本试题主要考查了三角函数的图像与性质的综合运用,奇偶性和单调性以及对称性的综合问题。
(1)因为函数 为偶函数,所以
为偶函数,所以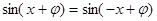 ,
,
所以解得 ,
,
(2)将函数化为单一三角函数


然后根据正切函数性质得到单调区间。
(3)
因为 ,所以
,所以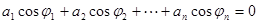 与
与 不能同时成立,
不能同时成立,
由 的图像关于点
的图像关于点 对称知道
对称知道 ,
, ,解得参数的值。
,解得参数的值。
解:(1)因为函数 为偶函数,所以
为偶函数,所以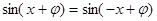 ,
,





 2分
2分
 ,
, ,
,
所以 ,
,






 4分
4分
(2)


 6分
6分
 ,其中
,其中 ,所以
,所以 ,
,






 8分
8分



由题意可知: ,
, ,
,
所以 ,
,






 10分
10分
(3)






















 12分
12分
因为 ,所以
,所以 与
与 不能同时成立,不妨设
不能同时成立,不妨设 ,
, ,
,
所以  ,其中
,其中 ;
;
由 的图像关于点
的图像关于点 对称,在
对称,在 处取得最小值,
处取得最小值, ,
, ,
,  , 所以,
, 所以, ,
,
 ①
①












 14分
14分
由 的图像关于点
的图像关于点 对称知道
对称知道 ,
, ,
, ,
, ,又因为
,又因为 在
在 处取得最小值,
处取得最小值,
所以 ,
, ,
,
所以
 ②
②












 16分
16分
由①②可知, ,
, 。
。






 18分
18分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
方体的长、宽、高各为多少时,其体积最大?最大体积是多少?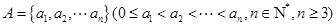 具有性质
具有性质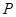 :对任意
:对任意 ,
,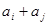 与
与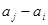 至少一个属于
至少一个属于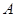 .
.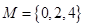 与
与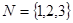 是否具有性质
是否具有性质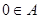 ;
;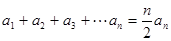 ;
;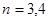 和
和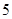 时,集合
时,集合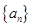 是否一定成等差数列.
是否一定成等差数列.