题目内容
已知函数f(x)= (m,n∈R)在x=1处取到极值2.
(m,n∈R)在x=1处取到极值2.
(1)求f(x)的解析式;
(2)设函数g(x)=ax-lnx.若对任意的x1∈[ ,2],总存在唯一的x2∈[
,2],总存在唯一的x2∈[ ,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围.
,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围.
 (m,n∈R)在x=1处取到极值2.
(m,n∈R)在x=1处取到极值2.(1)求f(x)的解析式;
(2)设函数g(x)=ax-lnx.若对任意的x1∈[
 ,2],总存在唯一的x2∈[
,2],总存在唯一的x2∈[ ,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围.
,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围.解: (1)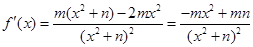 …………………………2分
…………………………2分
由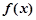 在
在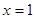 处取到极值2,故
处取到极值2,故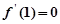 ,
,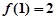 即
即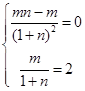 ,
,
解得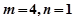 ,经检验,此时
,经检验,此时 在
在 处取得极值.故
处取得极值.故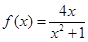 ……5分
……5分
(2)由(1)知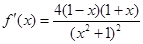 ,故
,故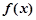 在
在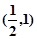 上单调递增,在
上单调递增,在
 上单调递减,由
上单调递减,由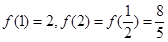 ,故
,故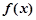 的值域为
的值域为 …………………………7分
…………………………7分
依题意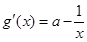 ,记
,记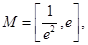
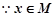
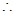

(ⅰ)当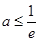 时,
时,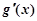
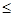
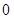 ,
,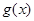 在
在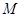 上单调递减,
上单调递减,
依题意由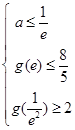 ,得
,得 ,……………………………………………………8分
,……………………………………………………8分
(ⅱ)当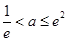 时,
时,
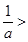
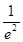 当
当 时,
时,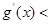
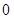 ,当
,当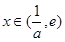 时,
时,
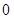
依题意得: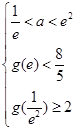 或
或 ,解得
,解得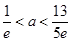 ,…………………………10分
,…………………………10分
(ⅲ)当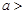
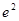 时,
时,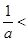
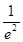 ,此时
,此时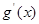
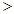
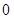 ,
,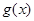 在
在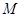 上单调递增依题意得
上单调递增依题意得
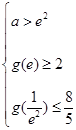 即
即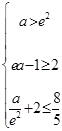 此不等式组无解 ……………………………………11分.
此不等式组无解 ……………………………………11分.
综上,所求 取值范围为
取值范围为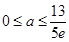 ………………………………………………14分
………………………………………………14分
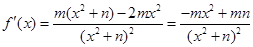 …………………………2分
…………………………2分由
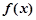 在
在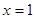 处取到极值2,故
处取到极值2,故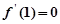 ,
,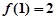 即
即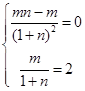 ,
,
解得
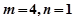 ,经检验,此时
,经检验,此时 在
在 处取得极值.故
处取得极值.故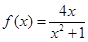 ……5分
……5分(2)由(1)知
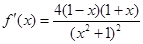 ,故
,故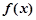 在
在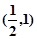 上单调递增,在
上单调递增,在
 上单调递减,由
上单调递减,由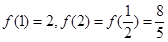 ,故
,故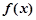 的值域为
的值域为 …………………………7分
…………………………7分依题意
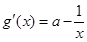 ,记
,记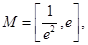
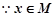
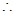

(ⅰ)当
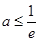 时,
时,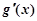
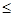
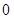 ,
,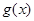 在
在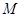 上单调递减,
上单调递减,依题意由
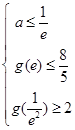 ,得
,得 ,……………………………………………………8分
,……………………………………………………8分(ⅱ)当
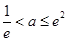 时,
时,
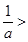
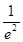 当
当 时,
时,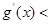
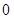 ,当
,当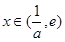 时,
时,
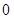
依题意得:
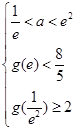 或
或 ,解得
,解得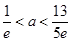 ,…………………………10分
,…………………………10分(ⅲ)当
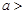
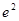 时,
时,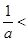
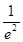 ,此时
,此时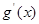
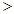
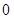 ,
,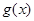 在
在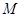 上单调递增依题意得
上单调递增依题意得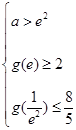 即
即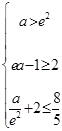 此不等式组无解 ……………………………………11分.
此不等式组无解 ……………………………………11分.综上,所求
 取值范围为
取值范围为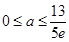 ………………………………………………14分
………………………………………………14分略

练习册系列答案
相关题目
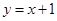 ; (2)
; (2)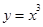 ; (3)
; (3)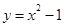 ; (4)
; (4)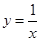 ,
,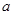 是抛掷一枚骰子得到的点数,则方程
是抛掷一枚骰子得到的点数,则方程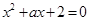 有两个不相等的实数根的概率为 .
有两个不相等的实数根的概率为 .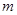 ,用抽气机抽x次后,剩余空气总量为
,用抽气机抽x次后,剩余空气总量为
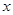 的函数关系式,并标明定义域;
的函数关系式,并标明定义域; ?
? )
)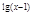 的定义域相同的函数是
的定义域相同的函数是


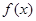 对一切实数
对一切实数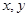 都有
都有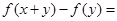
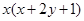 成立,且
成立,且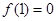 .
.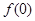 的值;
的值;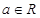 ,设P:当
,设P:当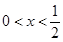 时,不等式
时,不等式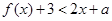 恒成立;Q:当
恒成立;Q:当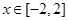 时,
时,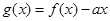 是单调函数。如果满足使P成立的
是单调函数。如果满足使P成立的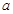 的集合记为
的集合记为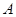 ,满足使Q成立的
,满足使Q成立的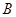 ,求
,求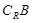 (
(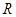 为全集)。
为全集)。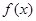 在
在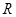 上是奇函数,且满足
上是奇函数,且满足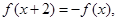 当
当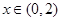 时,
时,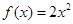 ,则
,则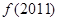 等于 ( )
等于 ( ) 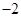
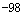
 ,则f(x)+f(1-x)=______,并利用推导等差数列前n项和公式的方法,求得f(-5)+f(-4)+···+f(0)+···+f(5)+f(6)的值为________
,则f(x)+f(1-x)=______,并利用推导等差数列前n项和公式的方法,求得f(-5)+f(-4)+···+f(0)+···+f(5)+f(6)的值为________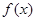 满足
满足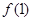 ="1" 且
="1" 且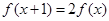 ,则
,则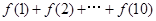 =_________
=_________