题目内容
已知:函数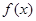 对一切实数
对一切实数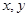 都有
都有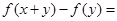
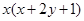 成立,且
成立,且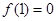 .
.
(1)求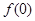 的值;
的值;
(2)求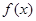 的解析式。
的解析式。
(3)已知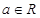 ,设P:当
,设P:当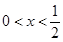 时,不等式
时,不等式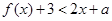 恒成立;Q:当
恒成立;Q:当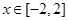 时,
时,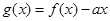 是单调函数。如果满足使P成立的
是单调函数。如果满足使P成立的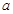 的集合记为
的集合记为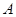 ,满足使Q成立的
,满足使Q成立的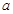 的集合记为
的集合记为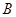 ,求
,求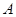 ∩
∩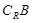 (
(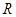 为全集)。
为全集)。
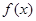 对一切实数
对一切实数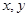 都有
都有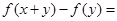
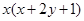 成立,且
成立,且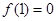 .
.(1)求
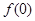 的值;
的值;(2)求
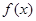 的解析式。
的解析式。 (3)已知
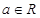 ,设P:当
,设P:当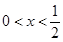 时,不等式
时,不等式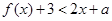 恒成立;Q:当
恒成立;Q:当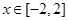 时,
时,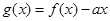 是单调函数。如果满足使P成立的
是单调函数。如果满足使P成立的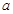 的集合记为
的集合记为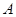 ,满足使Q成立的
,满足使Q成立的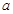 的集合记为
的集合记为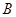 ,求
,求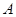 ∩
∩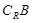 (
(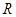 为全集)。
为全集)。解:
(1)令x=1,y="0" ∴f(1)-f(0)="2 " ∴f(0)="f(1)-2=-2 " ……
 …………
………… 3分
3分
(2) 令y="0" ∴f(x)-f(0)=x·(x+1) ∴f(x)=x2+x-2 ………………3分
令y="0" ∴f(x)-f(0)=x·(x+1) ∴f(x)=x2+x-2 ………………3分
(3)由P :∵f(x)+3<2x+a恒成立
:∵f(x)+3<2x+a恒成立
∴x2+x+1<2x+a

∴a>x2-x+1对 恒成立
恒成立
由Q:∵g(x)=x2+(1-a)x-2

B={a|a≥5或a≤-3}
 ………………4分
………………4分
(1)令x=1,y="0" ∴f(1)-f(0)="2 " ∴f(0)="f(1)-2=-2 " ……

 …………
………… 3分
3分(2)
 令y="0" ∴f(x)-f(0)=x·(x+1) ∴f(x)=x2+x-2 ………………3分
令y="0" ∴f(x)-f(0)=x·(x+1) ∴f(x)=x2+x-2 ………………3分(3)由P
 :∵f(x)+3<2x+a恒成立
:∵f(x)+3<2x+a恒成立∴x2+x+1<2x+a

|
 恒成立
恒成立
由Q:∵g(x)=x2+(1-a)x-2

B={a|a≥5或a≤-3}
 ………………4分
………………4分略

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 (m,n∈R)在x=1处取到极值2.
(m,n∈R)在x=1处取到极值2. ,2],总存在唯一的x2∈[
,2],总存在唯一的x2∈[ ,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围.
,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围. , 则Q(x)是( * )
, 则Q(x)是( * )

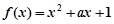 图象上一点
图象上一点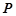 到直线
到直线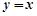 的距离的最小值为
的距离的最小值为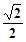 ,则
,则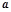 的值为 ▲ .
的值为 ▲ . ,则
,则 的最大值为_
的最大值为_  ,从A到B的映射
,从A到B的映射 ,在映射下,B中的元素为(1,1)对应的A中元素为
,在映射下,B中的元素为(1,1)对应的A中元素为 

 ,
, ,则
,则 = .
= . 是偶函数,且
是偶函数,且 时,
时, .求
.求 的值,
的值, 时
时 的值;
的值; )当
)当