题目内容
(本题满分15分)已知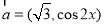 ,
,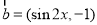 ,
,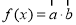
(1)求函数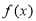 的单调增区间;
的单调增区间;
(2)当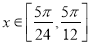 时,求函数
时,求函数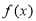 的值域.
的值域.
(1) ;(2)
;(2) .
.
【解析】
试题分析:先利用平面向量的数量积运算化简 成
成 的形式,再利用整体思想与三角函数的图像与性质进行求解.
的形式,再利用整体思想与三角函数的图像与性质进行求解.
试题解析:
(1)令 得
得
 ,
,
所以函数的单调递增区间为
当 时,
时, ,
, ,
,
当 时,函数
时,函数 的值域为
的值域为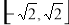 .
.
考点:1.平面向量的数量积;2.函数的单调区间;3.函数的值域.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
(本题满分15分)已知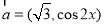 ,
,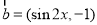 ,
,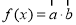
(1)求函数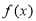 的单调增区间;
的单调增区间;
(2)当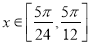 时,求函数
时,求函数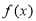 的值域.
的值域.
(1) ;(2)
;(2) .
.
【解析】
试题分析:先利用平面向量的数量积运算化简 成
成 的形式,再利用整体思想与三角函数的图像与性质进行求解.
的形式,再利用整体思想与三角函数的图像与性质进行求解.
试题解析:
(1)令 得
得
 ,
,
所以函数的单调递增区间为
当 时,
时, ,
, ,
,
当 时,函数
时,函数 的值域为
的值域为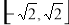 .
.
考点:1.平面向量的数量积;2.函数的单调区间;3.函数的值域.

 阅读快车系列答案
阅读快车系列答案