题目内容
20.求下列函数的定义域.(1)y=${x}^{-\frac{1}{3}}$
(2)y=${x}^{\frac{3}{4}}$
(3)y=(x2-3x)-3+1
(4)y=${{(x}^{2}-3x+2)}^{-\frac{1}{2}}$.
分析 根据分母不为0以及根式的意义,分别求出它们的定义域即可.
解答 解:(1)y=${x}^{-\frac{1}{3}}$=$\frac{1}{\root{3}{x}}$,∴函数的定义域是{x|x≠0};
(2)y=${x}^{\frac{3}{4}}$=$\frac{1}{\root{4}{{x}^{3}}}$,∴函数的定义域是{x|x>0};
(3)y=(x2-3x)-3+1=$\frac{1}{{{(x}^{2}-3x)}^{3}}$+1,∴函数的定义域是{x|x≠0且x≠3};
(4)y=${{(x}^{2}-3x+2)}^{-\frac{1}{2}}$=$\frac{1}{\sqrt{{x}^{2}-3x+2}}$,
由x2-3x+2=(x-1)(x-2)>0,解得:x>2或x<1,
∴函数的定义域是(-∞,1)∪(2,+∞).
点评 本题考查了求函数的定义域问题,考查解不等式问题,是一道基础题.

练习册系列答案
相关题目
15.等差数列{an}中,a4+a6=-6,S3=-27,则a9的值为( )
| A. | 3 | B. | 5 | C. | -4 | D. | -2 |
12.若f(x)=5-3x(2<x≤4),则f(x)的值域为( )
| A. | R | B. | [-7,-1) | C. | (-7,-1] | D. | {-7,-1} |
9.数列{1+2n-1}的前n项的和为( )
| A. | 1+2n | B. | 2+2n | C. | n+2n-1 | D. | n+2+2n |
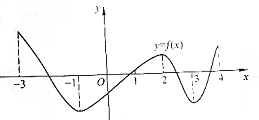 已知函数y=f(x)在区间[-3,4]上的图象如图所示,根据图象说出函数的单调区间,以及在每一个区间上函数的单调性.
已知函数y=f(x)在区间[-3,4]上的图象如图所示,根据图象说出函数的单调区间,以及在每一个区间上函数的单调性.