题目内容
6.已知x,y满足条件:$\left\{\begin{array}{l}7x-5y-23≤0\\ x+7y-11≤0\\ 4x+y+10≥0\end{array}\right.$,求:(1)4x-3y的最小值;
(2)$\frac{x-y+1}{x+5}$的取值范围.
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,进行求最值即可.
解答 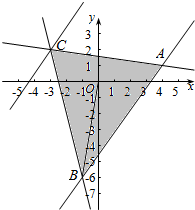 解:(1)不等式组$\left\{\begin{array}{l}7x-5y-23≤0\\ x+7y-11≤0\\ 4x+y+10≥0\end{array}\right.$表示的公共区域如图所示:
解:(1)不等式组$\left\{\begin{array}{l}7x-5y-23≤0\\ x+7y-11≤0\\ 4x+y+10≥0\end{array}\right.$表示的公共区域如图所示:
其中A(4,1)、B(-1,-6)、C(-3,2),
设z=4x-3y,则y=$\frac{4}{3}$x-$\frac{z}{3}$,平移直线y=$\frac{4}{3}$x-$\frac{z}{3}$,
由图象可知当直线y=$\frac{4}{3}$x-$\frac{z}{3}$过C点时,直线的截距最大,此时z取得最小值,
将C(-3,2),代入z=4x-3y得最小值,
即z的最小值z=4×(-3)-3×2=-18.
(2)$\frac{x-y+1}{x+5}$=$\frac{x+5-(y+4)}{x+5}$=1-$\frac{y+4}{x+5}$,
设k=$\frac{y+4}{x+5}$,则k的几何意义是动点(x,y)到定点D(-5,-4)的斜率,
而KCD=$\frac{-4-2}{-5+3}$=3,KBD=$\frac{-4+6}{-5+1}$=-$\frac{1}{2}$,
∴-$\frac{1}{2}$≤k≤3,
∴-2≤1-k≤$\frac{3}{2}$,
即$\frac{x-y+1}{x+5}$的取值范围是[-2,$\frac{3}{2}$].
点评 本题主要考查线性规划的基本应用,利用目标函数的几何意义是解决问题的关键,利用数形结合是解决问题的基本方法.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
14.设a=2-0.5,b=log20152016,c=sin1830°,则a,b,c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | b>a>c |
11.已知f(x)是定义在R上的偶函数,当x∈(-∞,0)时,f(x)=x-x2,则当x∈(0,+∞)时,f(x)的表达式为( )
| A. | x+x2 | B. | -x+x2 | C. | -x-x2 | D. | x-x2 |
18.已知函数y=log2(ax2-4x+4)的定义域为R,则实数a的取值范围是( )
| A. | (0,1] | B. | [0,1] | C. | [1,+∞) | D. | (1,+∞) |