题目内容
【题目】已知椭圆
的中心在原点，焦点在
轴，焦距为2，且长轴长是短轴长的
倍．
（1）求椭圆
的标准方程；
（2）设
，过椭圆
左焦点
的直线
交
于
、
两点，若对满足条件的任意直线
，不等式
（
）恒成立，求
的最小值．
【答案】（1）
（2）
的最小值为
【解析】
试题分析：（1）依题意，求出
，
，可得椭圆
的标准方程；（2）设
，
，可得
，首先讨论当直线
垂直于
轴时， 
．
当直线
不垂直于
轴时，设直线
：
，与椭圆方程联立，得到
，
，则，将
及，代入可得
，要使不等式
（
）恒成立，只需
，即的最小值为．
试题解析：（1）依题意，
，
，
解得
，
，∴椭圆
的标准方程为．
（2）设，，所以
，
当直线垂直于轴时，
，
且
，此时
，
，
所以
．
当直线不垂直于轴时，设直线：，
由
整理得
，
所以，，
所以
．
要使不等式（）恒成立，只需，即的最小值为．
期末集结号系列答案
【题目】衡州市英才中学贯彻党的教育方针，促进学生全面发展，积极组织开展了丰富多样的社团活动，根据调查，英才中学在传统民族文化的继承方面开设了“泥塑”、“剪纸”、“曲艺”三个社团，三个社团参加的人数如下表所示：
社团 | 泥塑 | 剪纸 | 曲艺 |
人数 | 320 | 240 | 200 |
为调查社团开展情况，学校社团管理部采用分层抽样的方法从中抽取一个容量为
的样本，已知从“剪纸”社团抽取的同学比从“泥塑”社团抽取的同学少2人。
（1）求三个社团分别抽取了多少同学；
（2）若从“剪纸”社团抽取的同学中选出2人担任该社团活动监督的职务，已知“剪纸”社团被抽取的同学中有2名女生，求至少有1名女同学被选为监督职务的概率.
【题目】为了解某单位员工的月工资水平，从该单位500位员工中随机抽取了50位进行调查，得到如下频数分布表和频率分布直方图：
月工资 （单位：百元） | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |
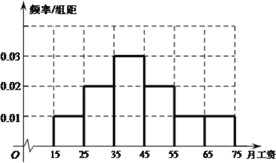
(1)
试由上图估计该单位员工月平均工资；
(2)现用分层抽样的方法从月工资在
和
的两组所调查的男员工中随机选取5人，问各应抽取多少人？
(3)若从月工资在
和两组所调查的女员工中随机选取2人，试求这2人月工资差不超过1000元的概率．
【题目】海关对同时从
，
，
三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量（单位：件）如下表所示．工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测．
地区 |
|
|
|
数量 | 50 | 150 | 100 |
（1）求这6件样品中来自
，
，
各地区商品的数量；
（2）若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．
