题目内容
集合A={x|x2-ax+a2-19=0},B={x|x2-5x+6=0},C={x|x2+2x-8=0}.
(1)若A∩B=A∪B,求a的值;
(2)若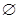
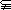 A∩B,A∩C=
A∩B,A∩C=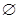 ,求a的值.
,求a的值.
(1)a=5(2)a=-2
解析试题分析:(1)先化简集合B和集合C,在再进行集合间的有关运算.(2)一定要注意特殊集合—空集.
由已知,得B={2,3},C={2,-4}
(1)∵A∩B=A∪B,∴A=B
∴2,3是一元二次方程x2-ax+a2-19=0的两个根,
由 解得a=5.
解得a=5.
(2)由A∩B 
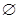
 ∩
∩
 ,又A∩C=
,又A∩C=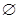 ,得3∈A,2
,得3∈A,2 A,-4
A,-4 A,
A,
由3∈A,得32-3a+a2-19=0,解得a=5或a=-2
当a=5时,A={x|x2-5x+6=0}={2,3},与2 A矛盾;
A矛盾;
当a=-2时,A={x|x2+2x-15=0}={3,-5},符合题意.
∴a=-2.
考点:集合的概念及运算.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 。
。 ;
; ,求实数a的取值范围。
,求实数a的取值范围。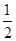 x2-x+
x2-x+ ,0≤x≤3}.
,0≤x≤3}.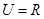 ,集合
,集合 ,
,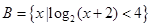 .
.
 ,若
,若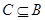 ,求实数
,求实数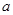 的取值范围.
的取值范围. 为函数的定义域,集合
为函数的定义域,集合 为函数的值域,集合
为函数的值域,集合 为不等式的解集.
为不等式的解集. ;w.w.w.zxxk.c.o. m
;w.w.w.zxxk.c.o. m 的取值范围.
的取值范围. ,集合
,集合 .
. ;
; ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.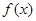 =
=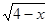
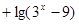 的定义域为
的定义域为 ,集合
,集合 =
= ,
, ,求
,求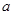 的取值范围.
的取值范围. ,集合B=
,集合B= ,全集U=R,
,全集U=R, .
.