题目内容
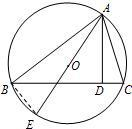
如图，△ABC是圆内接三角形，圆心O在BC上，若AB=6，BD=3.6，将一颗豆子随机地扔到该圆内，用M表示事件“豆子落在△ABC内”，N表示事件“豆子落在△ABD内”，则P（M）=| 24 |
| 25π |
| 24 |
| 25π |
0.36
0.36
．分析：由射影定理，得AB2=BD•BC，由此能求出P（M）和P（N|M）．
解答：解：由射影定理，得AB2=BD•BC，
∵AB=6，BD=3.6，
∴BC=10，AC=8，AD=4.8，
所以S△ABC=
×10×4.8=24，S圆O=25π，S△ABD=
×3.6×4.8=8.64，
∴P（M）=
=
，P（N/M）=
=0.36．
∵AB=6，BD=3.6，
∴BC=10，AC=8，AD=4.8，
所以S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴P（M）=
| S△ABC |
| S圆O |
| 24 |
| 25π |
| ||
|
点评：本题考查直角三角形的射影定理及几何概型的应用，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
相关题目
11、如图，△ABC是圆的内接三角形，PA切圆于点A，PB交圆于点D．若∠ABC=60°，PD=1，BD=8，则∠PAC=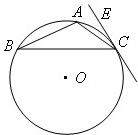
如图，△ABC是圆O的内接三角形，圆O的半径r=1，AB=1，BC=