题目内容
设 是椭圆
是椭圆 :
: 的左右焦点,
的左右焦点, 为直线
为直线 上一点,
上一点, 是底角为30°的等腰三角形,则
是底角为30°的等腰三角形,则 的离心率为( )
的离心率为( )
 是椭圆
是椭圆 :
: 的左右焦点,
的左右焦点, 为直线
为直线 上一点,
上一点, 是底角为30°的等腰三角形,则
是底角为30°的等腰三角形,则 的离心率为( )
的离心率为( )A. | B. | C. | D. |
C
试题分析:利用△F2PF1是底角为30°的等腰三角形,可得|PF2|=|F2F1|,根据P为直线
 上一点,可建立方程,由此可求椭圆的离心率.解:∵△F2PF1是底角为30°的等腰三角形,∴|PF2|=|F2F1|,∵P为直线
上一点,可建立方程,由此可求椭圆的离心率.解:∵△F2PF1是底角为30°的等腰三角形,∴|PF2|=|F2F1|,∵P为直线 上一点,∴2(
上一点,∴2( a-c)=2c,∴e=,
a-c)=2c,∴e=, =
= 故选C.
故选C.点评:本题考查椭圆的几何性质,解题的关键是确定几何量之间的关系,属于基础题

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
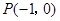 作曲线
作曲线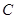 :
: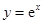 的切线,切点为
的切线,切点为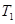 ,设
,设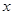 轴上的投影是点
轴上的投影是点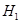 ,过点
,过点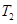 ,设
,设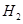 ,…,依次下去,得到第
,…,依次下去,得到第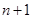
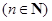 个切点
个切点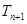 .则点
.则点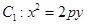 的焦点在抛物线
的焦点在抛物线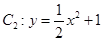 上.
上.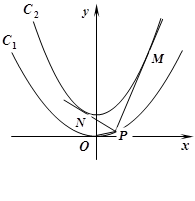
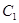 的方程及其准线方程;
的方程及其准线方程;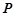 作抛物线
作抛物线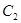 的两条切线
的两条切线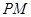 、
、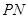 , 切点为
, 切点为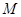 、
、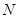 .若
.若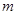 ,且
,且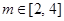 ,求
,求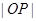 的取值范围.
的取值范围.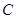 :
: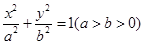 的焦距为
的焦距为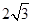 ,离心率为
,离心率为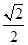 ,其右焦点为
,其右焦点为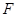 ,过点
,过点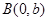 作直线交椭圆于另一点
作直线交椭圆于另一点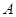 .
.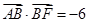 ,求
,求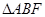 外接圆的方程;
外接圆的方程;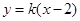 与椭圆
与椭圆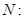
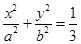 相交于两点
相交于两点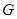 、
、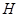 ,且
,且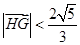 ,求
,求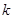 的取值范围.
的取值范围.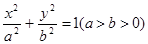 的左焦点为
的左焦点为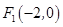 ,直线
,直线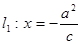 与
与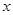 轴交于点
轴交于点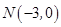 ,过点
,过点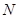 且倾斜角为30°的直线
且倾斜角为30°的直线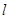 交椭圆于
交椭圆于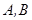 两点.
两点.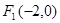 在以线段
在以线段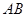 为直径的圆上;
为直径的圆上;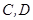 ,以
,以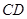 为直径且过点
为直径且过点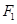 的所有圆中,求面积最小的圆的半径长.
的所有圆中,求面积最小的圆的半径长.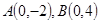 ,动点
,动点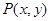 满足
满足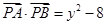 .
.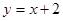 交于点
交于点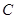 、
、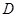 两点 ,求证
两点 ,求证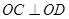 (
( 为原点)。
为原点)。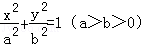 的离心率为
的离心率为 ,右焦点为F,且椭圆E上的点到点F距离的最小值为2.
,右焦点为F,且椭圆E上的点到点F距离的最小值为2.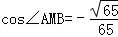 ,求△ABM的面积.
,求△ABM的面积. 的左右焦点为
的左右焦点为 ,直线AB过点
,直线AB过点 且交椭圆于A、B两点,则△
且交椭圆于A、B两点,则△ 的周长为_____________
的周长为_____________ 中,设点
中,设点 (
( ),直线
),直线 :
: ,点
,点 在直线
在直线 是线段
是线段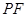 与
与 轴的交点, 过
轴的交点, 过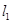 、
、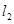 ,使
,使 ,
,
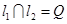 .
.
 的轨迹
的轨迹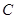 的方程;
的方程; 做曲线
做曲线 、
、 ,求证:直线
,求证:直线 恒过一定点;
恒过一定点; 的斜率存在时,直线
的斜率存在时,直线