题目内容
(本题满分15分)
已知函数 ,
,
(1)求函数的定义域;
(2)判断函数的奇偶性,并给予证明;
(3)求不等式 的解集.
的解集.
已知函数
 ,
,(1)求函数的定义域;
(2)判断函数的奇偶性,并给予证明;
(3)求不等式
 的解集.
的解集.解:(1)真数部分大于零,即解不等式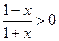 …………………………..2分
…………………………..2分
解得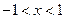 …………………………..4分
…………………………..4分
函数的定义域为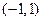 …………………………..5分
…………………………..5分
(2)函数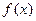 为奇函数…………………………..6分
为奇函数…………………………..6分
证明:由第一问函数的定义域为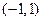 …………………………..7分
…………………………..7分
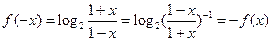 …………………………..9分
…………………………..9分
所以函数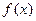 为奇函数…………………………..10分
为奇函数…………………………..10分
(3)解不等式
即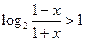 …………………………..分
…………………………..分
即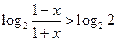 …………………………..11分
…………………………..11分
从而有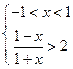 …………………………..12分
…………………………..12分
所以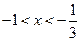 …………………………..14分
…………………………..14分
不等式 的解集为
的解集为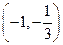 …………………………..15分
…………………………..15分
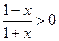 …………………………..2分
…………………………..2分解得
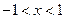 …………………………..4分
…………………………..4分函数的定义域为
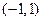 …………………………..5分
…………………………..5分(2)函数
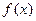 为奇函数…………………………..6分
为奇函数…………………………..6分证明:由第一问函数的定义域为
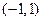 …………………………..7分
…………………………..7分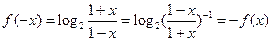 …………………………..9分
…………………………..9分所以函数
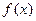 为奇函数…………………………..10分
为奇函数…………………………..10分(3)解不等式

即
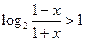 …………………………..分
…………………………..分即
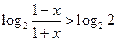 …………………………..11分
…………………………..11分从而有
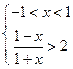 …………………………..12分
…………………………..12分所以
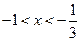 …………………………..14分
…………………………..14分不等式
 的解集为
的解集为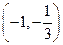 …………………………..15分
…………………………..15分略

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 是二次方程
是二次方程 的两个不同实根,
的两个不同实根, 是二次方程
是二次方程 的两个不同实根,若
的两个不同实根,若 ,则 ( )
,则 ( )  ,
,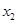 介于
介于 和
和 之间
之间 下表分段累计计算:
下表分段累计计算: )
) 元关于其当月工资
元关于其当月工资 元的函数
元的函数
 ,则
,则 = .
= .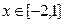 时,函数
时,函数 的值域是___________
的值域是___________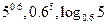 三者的大小关系是__ ▲ ___ (用“
三者的大小关系是__ ▲ ___ (用“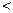 ”连接)
”连接)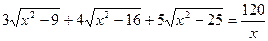 的解集______________
的解集______________