题目内容
(1)计算π0+2lg2+lg25-2sin2
+tan600°
(2)A是锐角三角形ABC的一个内角,且满足sinA+2cosA=2,求sinA•cosA值.
| 7π | 4 |
(2)A是锐角三角形ABC的一个内角,且满足sinA+2cosA=2,求sinA•cosA值.
分析:(1)原式第1项利用零指数幂法则计算,2、3项结合利用对数的运算性质化简,后两项利用诱导公式及 特殊角的三角函数值计算即可得到结果;
(2)已知等式变形表示出sinA,两边平方并利用同角三角函数间的基本关系化简,求出cosA的值,进而求出sinA的值,即可确定出所求式子的值.
(2)已知等式变形表示出sinA,两边平方并利用同角三角函数间的基本关系化简,求出cosA的值,进而求出sinA的值,即可确定出所求式子的值.
解答:解:(1)原式=1+2-1+
=2+
;
(2)由sinA+2cosA=2,得:sinA=2-2cosA,
两边平方得:sin2A=(2-2cosA)2,
又∵sin2A=1-cos2A,
∴1-cos2A=(2-2cosA)2,
化简整理得:5cos2A-8cosA+3=0,
即(cosA-1)(5cosA-3)=0,
∵A是锐角三角形ABC的一个内角,
∴cosA=
(cosA=1舍去),
∴sinA=2-2cosA=
,
则sinA•cosA=
.
| 3 |
| 3 |
(2)由sinA+2cosA=2,得:sinA=2-2cosA,
两边平方得:sin2A=(2-2cosA)2,
又∵sin2A=1-cos2A,
∴1-cos2A=(2-2cosA)2,
化简整理得:5cos2A-8cosA+3=0,
即(cosA-1)(5cosA-3)=0,
∵A是锐角三角形ABC的一个内角,
∴cosA=
| 3 |
| 5 |
∴sinA=2-2cosA=
| 4 |
| 5 |
则sinA•cosA=
| 12 |
| 25 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
 某潜水员身背氧气瓶潜入湖底进行考察,氧气瓶形状如图,其结构为一个圆柱和一个圆台的组合(设氧气瓶中氧气已充满,所给尺寸是氧气瓶的内径尺寸),潜水员在潜入水下a米的过程中,速度为v米/分,每分钟需氧量与速度平方成正比(当速度为1米/分时,每分钟需氧量为0.2L);在湖底工作时,每分钟需氧量为0.4L;返回水面时,速度也为v米/分,每分钟需氧量为0.2L,若下潜与上浮时速度不能超过p米/分,试问潜水员在湖底最多能工作多少时间?(氧气瓶体积计算精确到1L,a、p为常数,圆台的体积V=
某潜水员身背氧气瓶潜入湖底进行考察,氧气瓶形状如图,其结构为一个圆柱和一个圆台的组合(设氧气瓶中氧气已充满,所给尺寸是氧气瓶的内径尺寸),潜水员在潜入水下a米的过程中,速度为v米/分,每分钟需氧量与速度平方成正比(当速度为1米/分时,每分钟需氧量为0.2L);在湖底工作时,每分钟需氧量为0.4L;返回水面时,速度也为v米/分,每分钟需氧量为0.2L,若下潜与上浮时速度不能超过p米/分,试问潜水员在湖底最多能工作多少时间?(氧气瓶体积计算精确到1L,a、p为常数,圆台的体积V= 米的过程中,速度为
米的过程中,速度为 米/分,每分钟
米/分,每分钟 ,其中h为高,r、R分
,其中h为高,r、R分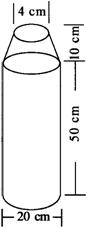
 某潜水员身背氧气瓶潜入湖底进行考察,氧气瓶形状如图,其结构为一个圆柱和一个圆台的组合(设氧气瓶中氧气已充满,所给尺寸是氧气瓶的内径尺寸),潜水员在潜入水下a米的过程中,速度为v米/分,每分钟需氧量与速度平方成正比(当速度为1米/分时,每分钟需氧量为0.2L);在湖底工作时,每分钟需氧量为0.4L;返回水面时,速度也为v米/分,每分钟需氧量为0.2L,若下潜与上浮时速度不能超过p米/分,试问潜水员在湖底最多能工作多少时间?(氧气瓶体积计算精确到1L,a、p为常数,圆台的体积V=
某潜水员身背氧气瓶潜入湖底进行考察,氧气瓶形状如图,其结构为一个圆柱和一个圆台的组合(设氧气瓶中氧气已充满,所给尺寸是氧气瓶的内径尺寸),潜水员在潜入水下a米的过程中,速度为v米/分,每分钟需氧量与速度平方成正比(当速度为1米/分时,每分钟需氧量为0.2L);在湖底工作时,每分钟需氧量为0.4L;返回水面时,速度也为v米/分,每分钟需氧量为0.2L,若下潜与上浮时速度不能超过p米/分,试问潜水员在湖底最多能工作多少时间?(氧气瓶体积计算精确到1L,a、p为常数,圆台的体积V=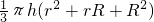 ,其中h为高,r、R分别为上、下底面半径.)
,其中h为高,r、R分别为上、下底面半径.) ,其中h为高,r、R分别为上、下底面半径.)
,其中h为高,r、R分别为上、下底面半径.)