题目内容
 某潜水员身背氧气瓶潜入湖底进行考察,氧气瓶形状如图,其结构为一个圆柱和一个圆台的组合(设氧气瓶中氧气已充满,所给尺寸是氧气瓶的内径尺寸),潜水员在潜入水下a米的过程中,速度为v米/分,每分钟需氧量与速度平方成正比(当速度为1米/分时,每分钟需氧量为0.2L);在湖底工作时,每分钟需氧量为0.4L;返回水面时,速度也为v米/分,每分钟需氧量为0.2L,若下潜与上浮时速度不能超过p米/分,试问潜水员在湖底最多能工作多少时间?(氧气瓶体积计算精确到1L,a、p为常数,圆台的体积V=
某潜水员身背氧气瓶潜入湖底进行考察,氧气瓶形状如图,其结构为一个圆柱和一个圆台的组合(设氧气瓶中氧气已充满,所给尺寸是氧气瓶的内径尺寸),潜水员在潜入水下a米的过程中,速度为v米/分,每分钟需氧量与速度平方成正比(当速度为1米/分时,每分钟需氧量为0.2L);在湖底工作时,每分钟需氧量为0.4L;返回水面时,速度也为v米/分,每分钟需氧量为0.2L,若下潜与上浮时速度不能超过p米/分,试问潜水员在湖底最多能工作多少时间?(氧气瓶体积计算精确到1L,a、p为常数,圆台的体积V=| 1 | 3 |
分析:氧气瓶中氧气的体积V=V圆柱+V圆台=π×102×50+π×10×
(4+20+100)≈5413π≈16997(cm3)≈17 L.设潜入水下a米过程中的每分钟需氧量为Q,则Q=kv2,因当速度为1 m/分时,每分钟需氧量0.2 L,所以k=0.2,故来回途中需氧量为a×0.2v+a×
,v∈(0,p],则在湖底的工作时间为
[17-(0.2av+
)].由此能够求出潜水员在湖底最多能工作多少时间.
| 1 |
| 3 |
| 0.2 |
| v |
| 1 |
| 0.4 |
| 0.2a |
| v |
解答:解:氧气瓶中氧气的体积
V=V圆柱+V圆台=π×102×50+π×10×
(4+20+100)≈5413π≈16997(cm3)≈17 L.
设潜入水下a米过程中的每分钟需氧量为Q,则Q=kv2,
因当速度为1 m/分时,每分钟需氧量0.2 L,所以k=0.2,
故来回途中需氧量为a×0.2v+a×
,v∈(0,p],
则在湖底的工作时间为
[17-(0.2av+
)],
∵0.2av+
≥0.4a,…..(6分)
当且仅当,v=1时取等号.
所以①当p≥1时,
[17-(0.2av+
)]的最大值是42.5-a.
②当p<1时,v∈(0,p],
∵v≤p<1,vp≤p2<1,
[17-(0.2av+
)]-
[17-(0.2ap+
)]=
(p-v)(
)≤0,
即当v=p时,在湖底的工作时间的最大值为
[17-(0.2ap+
)],
因此,当p≥1时,潜水员在湖底最多能工作42.5-a分钟;
当p<l时,潜水员在湖底最多能工作
[17-(0.2ap+
)]分钟.…(14分)
V=V圆柱+V圆台=π×102×50+π×10×
| 1 |
| 3 |
设潜入水下a米过程中的每分钟需氧量为Q,则Q=kv2,
因当速度为1 m/分时,每分钟需氧量0.2 L,所以k=0.2,
故来回途中需氧量为a×0.2v+a×
| 0.2 |
| v |
则在湖底的工作时间为
| 1 |
| 0.4 |
| 0.2a |
| v |
∵0.2av+
| 0.2 |
| v |
当且仅当,v=1时取等号.
所以①当p≥1时,
| 1 |
| 0.4 |
| 0.2a |
| v |
②当p<1时,v∈(0,p],
∵v≤p<1,vp≤p2<1,
| 1 |
| 0.4 |
| 0.2a |
| v |
| 1 |
| 0.4 |
| 0.2a |
| p |
| a |
| 2 |
| vp-1 |
| vp |
即当v=p时,在湖底的工作时间的最大值为
| 1 |
| 0.4 |
| 0.2a |
| p |
因此,当p≥1时,潜水员在湖底最多能工作42.5-a分钟;
当p<l时,潜水员在湖底最多能工作
| 1 |
| 0.4 |
| 0.2a |
| p |
点评:本题考查函数模型的选择和应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化,恰当地建立方程.易错点是弄不清数量间的相互关系,导致建立方程出错.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 某潜水员身背氧气瓶潜入湖底进行考察,氧气瓶形状如图,其结构为一个圆柱和一个圆台的组合(设氧气瓶中氧气已充满,所给尺寸是氧气瓶的内径尺寸),潜水员在潜入水下a米的过程中,速度为v米/分,每分钟需氧量与速度平方成正比(当速度为1米/分时,每分钟需氧量为0.2L);在湖底工作时,每分钟需氧量为0.4L;返回水面时,速度也为v米/分,每分钟需氧量为0.2L,若下潜与上浮时速度不能超过p米/分,试问潜水员在湖底最多能工作多少时间?(氧气瓶体积计算精确到1L,a、p为常数,圆台的体积V=
某潜水员身背氧气瓶潜入湖底进行考察,氧气瓶形状如图,其结构为一个圆柱和一个圆台的组合(设氧气瓶中氧气已充满,所给尺寸是氧气瓶的内径尺寸),潜水员在潜入水下a米的过程中,速度为v米/分,每分钟需氧量与速度平方成正比(当速度为1米/分时,每分钟需氧量为0.2L);在湖底工作时,每分钟需氧量为0.4L;返回水面时,速度也为v米/分,每分钟需氧量为0.2L,若下潜与上浮时速度不能超过p米/分,试问潜水员在湖底最多能工作多少时间?(氧气瓶体积计算精确到1L,a、p为常数,圆台的体积V=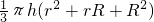 ,其中h为高,r、R分别为上、下底面半径.)
,其中h为高,r、R分别为上、下底面半径.) ,其中h为高,r、R分别为上、下底面半径.)
,其中h为高,r、R分别为上、下底面半径.)