题目内容
【题目】如图，在平面直角坐标系xOy中，椭圆C： 
+ 
=1（a＞b＞0）的左、右焦点分别为F1 ， F2 ， 点P（3，1）在椭圆上，△PF1F2的面积为2 
． 
（1）①求椭圆C的标准方程； ②若∠F1QF2= 
，求QF1QF2的值．
（2）直线y=x+k与椭圆C相交于A，B两点，若以AB为直径的圆经过坐标原点，求实数k的值．
【答案】
（1）解：①由条件，可设椭圆的标准方程为 
，将点P（3，1）代入椭圆方程，
∴ 
，
由 
= 
2c1=2 
，即 
又a2=b2+c2，
∴a2=12，b2=4，
∴椭圆的标准方程为： 
；
②当 
时，有 
∴ 
（2）解：设A（x1，y1），B（x2，y2），由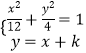 
，得4x2+6kx+3k2﹣12=0
由韦达定理及直线方程可知： 
，
∵以AB为直径的圆经过坐标原点，则 
，
解得： 
，此时△=120＞0，满足条件，
因此
【解析】（1）由三角形的面积 = 2c1，即可求得 
，将点P（3，1）代入椭圆方程，由椭圆的性质a2=b2+c2 ， 即可求得a和b的值，求得椭圆方程；当 时，根据椭圆的性质及完全平方公式，即可求得QF1QF2的值；（2）将直线方程代入椭圆方程，求得关于x的一元二次方程，由韦达定理求得x1x2及y1y2 ， 由题意可知 
=0，根据向量数量积的坐标运算，即可求得实数k的值．
【题目】某高校共有学生15000人，其中男生10500人，女生4500人，为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位：小时）．
（1）应收集多少位女生的样本数据？
（2）根据这300样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图所示），其中样本数据的分组区间为： 
．估计该校学生每周平均体育运动时间超过4小时的概率；
（3）在样本数据中，有60位女生的每周平均体育运动时间超过4小时，请完成每周平均体育运动时间与性别的列联表，并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”．
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
附： 
