题目内容
把长为10cm的细铁丝截成两段,各自围成一个正方形,求这两个正方形面积之和的最小值.
分析:设铁丝一段长xcm,0<x<10,两正方形面积之和为ycm2,则另一段铁丝长为(10-x)cm,依题意求得
y=
(x-5)2+
,再利用二次函数的性质求得它的最小值.
y=
| 1 |
| 8 |
| 25 |
| 8 |
解答:解:设铁丝一段长xcm,0<x<10,两正方形面积之和为ycm2,则另一段铁丝长为(10-x)cm,
依题意可得,y=(
)2+(
)2=
(x-5)2+
,
故当x=5时,y取最小值为
平方厘米.
依题意可得,y=(
| x |
| 4 |
| 10-x |
| 4 |
| 1 |
| 8 |
| 25 |
| 8 |
故当x=5时,y取最小值为
| 25 |
| 8 |
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,属于中档题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
把长为12cm的细铁丝截成两段,各自围成一个正三角形,那么这两个正三角形面积之和的最小值是( )
A、
| ||||
| B、4cm2 | ||||
C、3
| ||||
D、2
|

 cm2
cm2 cm2
cm2 cm2
cm2
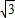 cm2
cm2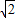 cm2
cm2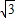 cm2
cm2