题目内容
已知椭圆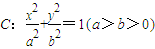 的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若
的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若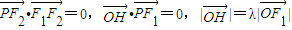 ,
,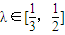 (其中O为坐标原点).求椭圆C离心率e的最大值.
(其中O为坐标原点).求椭圆C离心率e的最大值.
【答案】分析:由已知中椭圆 的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,
的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点, ,我们易得PF2⊥F1F2,OH⊥PF1,进而由
,我们易得PF2⊥F1F2,OH⊥PF1,进而由 ,我们可以得到离心率e平方的表达式,分析出其对应函数的单调性,进而得到椭圆C离心率e的最大值.
,我们可以得到离心率e平方的表达式,分析出其对应函数的单调性,进而得到椭圆C离心率e的最大值.
解答:解:由题意知PF2⊥F1F2,OH⊥PF1,则有△F1OH与△F1PF2相似,
所以 ,设F1(-c,0),F2(c,0),c>0,P(c,y1),
,设F1(-c,0),F2(c,0),c>0,P(c,y1),
则有 ,解得
,解得 ,
,
所以 .
.
根据椭圆的定义得: ,
,
∴ ,
,
即 ,
,
所以 ,
,
∵ 在
在 上是单调减函数,
上是单调减函数,
∴当 时,e2取最大值
时,e2取最大值 ,
,
所以椭圆C离心率e的最大值是 .
.
点评:本题考查的知识点是椭圆的标准方程,椭圆的简单性质,椭圆的离心率,其中由已知条件求出离心率e平方的表达式,并分析出其对应函数的单调性是解答本题的关键.
 的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,
的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点, ,我们易得PF2⊥F1F2,OH⊥PF1,进而由
,我们易得PF2⊥F1F2,OH⊥PF1,进而由 ,我们可以得到离心率e平方的表达式,分析出其对应函数的单调性,进而得到椭圆C离心率e的最大值.
,我们可以得到离心率e平方的表达式,分析出其对应函数的单调性,进而得到椭圆C离心率e的最大值.解答:解:由题意知PF2⊥F1F2,OH⊥PF1,则有△F1OH与△F1PF2相似,
所以
 ,设F1(-c,0),F2(c,0),c>0,P(c,y1),
,设F1(-c,0),F2(c,0),c>0,P(c,y1),则有
 ,解得
,解得 ,
,所以
 .
.根据椭圆的定义得:
 ,
,∴
 ,
,即
 ,
,所以
 ,
,∵
 在
在 上是单调减函数,
上是单调减函数,∴当
 时,e2取最大值
时,e2取最大值 ,
,所以椭圆C离心率e的最大值是
 .
.点评:本题考查的知识点是椭圆的标准方程,椭圆的简单性质,椭圆的离心率,其中由已知条件求出离心率e平方的表达式,并分析出其对应函数的单调性是解答本题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
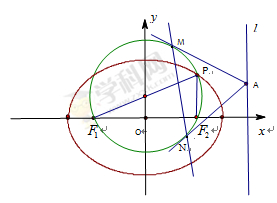
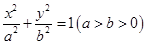 的左右两焦点分别为
的左右两焦点分别为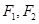 ,
, 是椭圆上一点,且在
是椭圆上一点,且在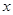 轴上方,
轴上方,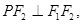
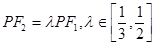 .
.
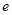 的取值范围;
的取值范围;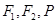 的圆
的圆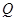 的截
的截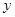 轴的线段长为6,求椭圆的方程;
轴的线段长为6,求椭圆的方程;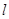 上任一点
上任一点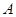 引圆
引圆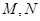 .试探究直线
.试探究直线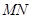 是否过定点?若过定点,请求出该定点;否则,请说明理由.
是否过定点?若过定点,请求出该定点;否则,请说明理由. 的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若
的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若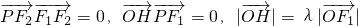 ,
,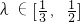 (其中O为坐标原点).求椭圆C离心率e的最大值.
(其中O为坐标原点).求椭圆C离心率e的最大值.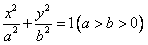 的左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,OH=λOF1,λ∈[
的左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,OH=λOF1,λ∈[ ,
, ]。
]。
 的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若
的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若 ,
, (其中O为坐标原点).
(其中O为坐标原点). ,求直线l的方程.
,求直线l的方程.