题目内容
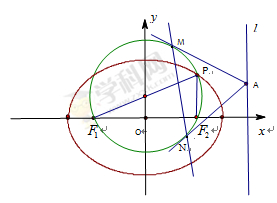
已知椭圆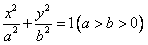 的左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,OH=λOF1,λ∈[
的左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,OH=λOF1,λ∈[ ,
, ]。
]。
(1)求椭圆的离心率e的取值范围;
(2)当e取最大值时,过F1,F2,P的圆Q的截y轴的线段长为6,求圆Q的方程;
(3)在(2)的条件下,过椭圆右准线L上任一点A引圆Q的两条切线,切点分别为M,N,试探究直线MN是否过定点?若过定点,请求出该定点;否则,请说明理由。
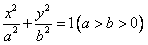 的左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,OH=λOF1,λ∈[
的左右两焦点为F1,F2,P是椭圆上一点,且在x轴上方,PF2⊥F1F2,OH⊥PF1于H,OH=λOF1,λ∈[ ,
, ]。
]。(1)求椭圆的离心率e的取值范围;
(2)当e取最大值时,过F1,F2,P的圆Q的截y轴的线段长为6,求圆Q的方程;
(3)在(2)的条件下,过椭圆右准线L上任一点A引圆Q的两条切线,切点分别为M,N,试探究直线MN是否过定点?若过定点,请求出该定点;否则,请说明理由。

解:由相似三角形知,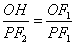 ,
,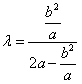 ,
,
∴ 。
。
(1)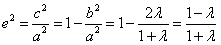 ,
,
∴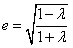 ,在
,在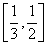 上单调递减,
上单调递减,
∴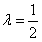 时,
时,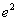 最小
最小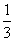 ,
,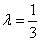 时,
时,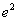 最小
最小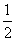 ,
,
∴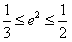 ,∴
,∴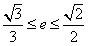 。
。
(2)当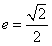 时,
时,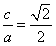 ,∴
,∴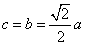 ,∴
,∴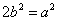 ,
,
∵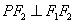 ,
,
∴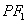 是圆的直径,圆心是
是圆的直径,圆心是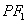 的中点,
的中点,
∴在y轴上截得的弦长就是直径,∴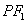 =6,
=6,
又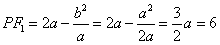 ,
,
∴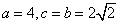 ,
,
∴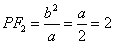 ,圆心Q(0,1),半径为3,
,圆心Q(0,1),半径为3,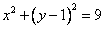 。
。
(3)椭圆方程是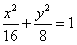 ,右准线方程为
,右准线方程为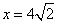 ,
,
∵直线AM,AN是圆Q的两条切线,
∴切点M,N在以AQ为直径的圆上。
设A点坐标为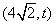 ,
,
∴该圆方程为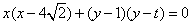 ,
,
∴直线MN是两圆的公共弦,两圆方程相减,得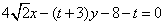 ,
,
这就是直线MN的方程,
该直线化为: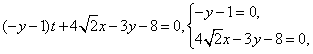 ,
,
∴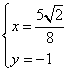 ,∴直线MN必过定点
,∴直线MN必过定点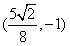 。
。

练习册系列答案
相关题目
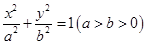 的左右两焦点分别为
的左右两焦点分别为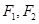 ,
, 是椭圆上一点,且在
是椭圆上一点,且在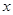 轴上方,
轴上方,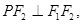
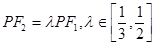 .
.
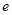 的取值范围;
的取值范围;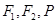 的圆
的圆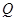 的截
的截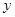 轴的线段长为6,求椭圆的方程;
轴的线段长为6,求椭圆的方程;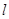 上任一点
上任一点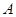 引圆
引圆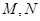 .试探究直线
.试探究直线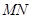 是否过定点?若过定点,请求出该定点;否则,请说明理由.
是否过定点?若过定点,请求出该定点;否则,请说明理由. 的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若
的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若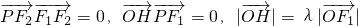 ,
,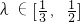 (其中O为坐标原点).求椭圆C离心率e的最大值.
(其中O为坐标原点).求椭圆C离心率e的最大值. 的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若
的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若 ,
, (其中O为坐标原点).
(其中O为坐标原点). ,求直线l的方程.
,求直线l的方程.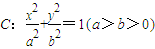 的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若
的左右两焦点分别为F1,F2,P是椭圆C上的一点,且在x轴的上方,H是PF1上一点,若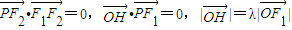 ,
,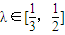 (其中O为坐标原点).求椭圆C离心率e的最大值.
(其中O为坐标原点).求椭圆C离心率e的最大值.