题目内容
已知抛物线L的方程为![]() ,直线
,直线![]() 截抛物线L所得弦长为
截抛物线L所得弦长为![]() .
.
(Ⅰ)求p的值;
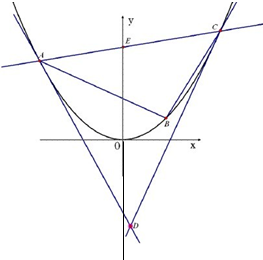
(Ⅱ)若直角三角形![]() 的三个顶点在抛物线L上,且直角顶点
的三个顶点在抛物线L上,且直角顶点![]() 的横坐标为1,过点
的横坐标为1,过点![]() 分别作抛物线L的切线,两切线相交于点
分别作抛物线L的切线,两切线相交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,当直线
,当直线![]() 的斜率在
的斜率在![]() 上变化时,直线
上变化时,直线![]() 斜率是否存在最大值,若存在,求其最大值和直线
斜率是否存在最大值,若存在,求其最大值和直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.

(Ⅰ) 解:(1)![]() ,
,![]() …………………………(5分)
…………………………(5分)
(Ⅱ) 解: B![]() ,设
,设![]() ,
,![]() ,
,![]()
设BC的斜率为k,则
![]() ,
,
又![]() ,C
,C![]() A
A![]()
![]() ,
,
直线AC的方程为![]() ,
,
令![]()
AD:![]()
同理CD:![]() ,联立两方程得D
,联立两方程得D![]()

令![]() 递减,所以,当
递减,所以,当![]() 时,
时,![]() 最大为
最大为![]()
所以,BC的方程为即![]() ……………(15分)
……………(15分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知抛物线L的方程为x2=2py(p>0),直线y=x截抛物线L所得弦长为
已知抛物线L的方程为x2=2py(p>0),直线y=x截抛物线L所得弦长为 .
.
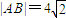 .
.