题目内容
已知抛物线L的方程为x2=2py（p＞0），直线y=x截抛物线L所得弦
．
（1）求p的值；
（2）抛物线L上是否存在异于点A、B的点C，使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线．若存在，求出点C的坐标；若不存在，请说明理由．
．（1）求p的值；
（2）抛物线L上是否存在异于点A、B的点C，使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线．若存在，求出点C的坐标；若不存在，请说明理由．
解：（1）由 
解得A（0，0），B（2p，2p）
∴
，
∴p=2
（2）由（1）得x2=4y，A（0，0），B（4，4）
假设抛物线L上存在异于点A、B的点C
，
使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线令圆的圆心为N（a，b），
则由
得
得
∵抛物线L在点C处的切线斜率
又该切线与NC垂直，
∴
∴
∵t≠0，t≠4，
∴t=﹣2 故存在点C且坐标为（﹣2，1）．
解得A（0，0），B（2p，2p） ∴
，∴p=2
（2）由（1）得x2=4y，A（0，0），B（4，4）
假设抛物线L上存在异于点A、B的点C
，使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线令圆的圆心为N（a，b），
则由
得
得
∵抛物线L在点C处的切线斜率
又该切线与NC垂直，
∴
∴ ∵t≠0，t≠4，
∴t=﹣2 故存在点C且坐标为（﹣2，1）．
练习册系列答案
相关题目
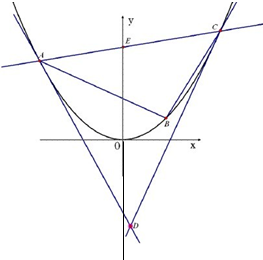已知抛物线L的方程为x2=2py（p＞0），直线y=x截抛物线L所得弦长为
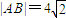，直线
截抛物线L所得弦长为
．
的三个顶点在抛物线L上，且直角顶点
的横坐标为1，过点
分别作抛物线L的切线，两切线相交于点
，直线
与
轴交于点
，当直线
的斜率在
上变化时，直线
斜率是否存在最大值，若存在，求其最大值和直线
．