题目内容
已知函数 ,
, .
.
(1)求函数 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)求函数 在区间
在区间 上的最小值和最大值;
上的最小值和最大值;
(3)若 ,求使
,求使 的
的 取值范围.
取值范围.
(1)函数 的单调增区间是
的单调增区间是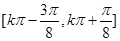 (
(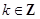 ),最小正周期为
),最小正周期为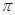 ;
;
(2) 在区间
在区间 上的最小值是
上的最小值是 ,最大值是
,最大值是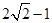 ;
;
(3)使 的
的 取值范围是
取值范围是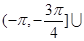
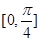
解析试题分析:(1)先对函数 利用三角恒等变换公式进行化简,再利用周期公式求周期;根据化简后的三角函数解析式,令
利用三角恒等变换公式进行化简,再利用周期公式求周期;根据化简后的三角函数解析式,令 ,
,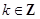 从中解出x的取值范围,即可得到函数的单调递减区间;
从中解出x的取值范围,即可得到函数的单调递减区间;
(3)由 得出的
得出的 取值范围,然后再由正弦函数的性质求出
取值范围,然后再由正弦函数的性质求出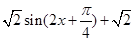 的
的 取值范围,.
取值范围,.
(3)由 得出的
得出的 取值范围,然后再由正弦函数的性质求出
取值范围,然后再由正弦函数的性质求出 中的取值范围,两者取交集即可得到
中的取值范围,两者取交集即可得到 取值范围.
取值范围.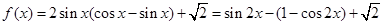
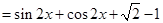
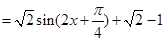
(1)函数 的最小正周期为
的最小正周期为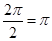 .
.
令 (
(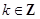 )得,
)得,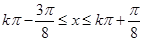 (
(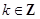 ).
).
所以函数 的单调增区间是
的单调增区间是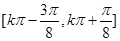 (
(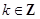 ).
).
(2)因为 ,所以
,所以 .
.
所以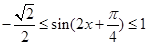 .
.
所以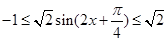 .
.
所以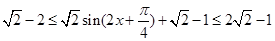 .
.
所以函数 在区间
在区间 上的最小值是
上的最小值是 ,最大值是
,最大值是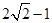 .
.
(3) 因为 ,所以
,所以 .
.
由 得,
得, ,
,
所以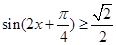 .
.
所以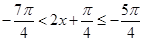 或
或 .
.
所以 或
或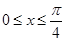 .
.
当 时,使
时,使 的
的 取值范围是
取值范围是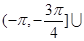
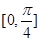 .
.
考点:正弦函数的性质及其应用

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
某同学用“五点法”画函数 在某一个周期内的图象时,列表并填入的部分数据如下表:
在某一个周期内的图象时,列表并填入的部分数据如下表:
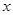 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
(1)请求出上表中的
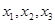 ,并直接写出函数
,并直接写出函数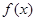 的解析式;
的解析式;(2)将
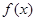 的图象沿
的图象沿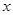 轴向右平移
轴向右平移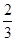 个单位得到函数
个单位得到函数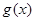 ,若函数
,若函数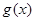 在
在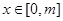 (其中
(其中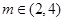 )上的值域为
)上的值域为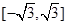 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为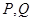 ,求
,求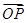 与
与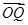 夹角
夹角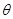 的大小。
的大小。  )-
)- sin2x+sinxcosx.
sin2x+sinxcosx. 对称,求m的最小正值.
对称,求m的最小正值.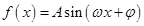 ,x∈R(其中A>0,ω>0,
,x∈R(其中A>0,ω>0, )的周期为π,且图象上一个最低点为M
)的周期为π,且图象上一个最低点为M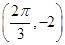 .
.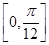 时,求f(x)的最大值.
时,求f(x)的最大值.
 ;
; 是第三象限角,且
是第三象限角,且 ,求
,求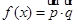 ,而
,而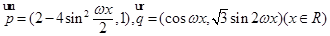 .
.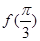 最大,求
最大,求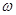 能取到的最小正数值.
能取到的最小正数值.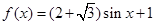 且
且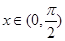 ,求
,求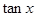 .
.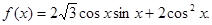
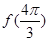 的值;
的值;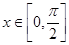 时,求函数
时,求函数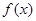 的值域.
的值域.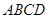 内修建一个三角形隔离区以投放净化物质,其形状为三角形
内修建一个三角形隔离区以投放净化物质,其形状为三角形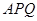 ,其中
,其中 位于边
位于边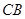 上,
上,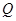 位于边
位于边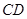 上.已知
上.已知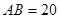 米,
米,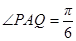 ,设
,设 ,记
,记 ,当
,当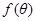 越大,则污水净化效果越好.
越大,则污水净化效果越好.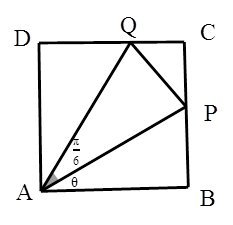
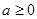 ,若
,若 的最大值为0,最小值为-4,试求
的最大值为0,最小值为-4,试求 与
与 的值,并求
的值,并求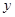 的最大、最小值及相应的
的最大、最小值及相应的 值.
值.