题目内容
A是单位圆与x轴正半轴的交点,B,P为圆上不同点,∠AOP=60°,∠AOB=θ,0≤θ<2π,
(1)当θ为何值时
=
;
(2)若
=
+
,且点Q在单位圆上求点Q的坐标;
(3)设a
+
的横坐标为f(θ),求f(θ)+2cos2θ的最小值.
(1)当θ为何值时
| AP |
| OB |
(2)若
| QO |
| OA |
| OB |
(3)设a
| OB |
| OP |
考点:平面向量数量积的运算,三角函数线
专题:平面向量及应用
分析:(1)由题意可得
=(-
,
),
=(cosθ,sinθ),可得当cosθ=-
,sinθ=
,
=
,并结合θ的范围,求得θ的值.
(2)设点Q(x,y),则
+
=(1+cosθ,sinθ),-x=1+cosθ,-y=sinθ,再由x2+y2=1求得cosθ 的值,可得θ的值.
(3)求得 a
+
的横坐标为f(θ)=a•cosθ+
,可得f(θ)+2cos2θ=2(cosθ+
)2+
-
,再分对称轴cosθ=-
在区间[-1,1]的左侧、中间、右侧三种情况,分别求得f(θ)+2cos2θ的最小值.
| AP |
| 1 |
| 2 |
| ||
| 2 |
| OB |
| 1 |
| 2 |
| ||
| 2 |
| AP |
| OB |
(2)设点Q(x,y),则
| OA |
| OB |
(3)求得 a
| OB |
| OP |
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| a2 |
| 8 |
| a |
| 2 |
解答:
解:(1)由题意可得A(1,0)、P(cos60°,sin60°)、B(cosθ,sinθ),
=(cos60°-1,sin60°-0)=(-
,
),
=(cosθ,sinθ),
故当cosθ=-
,sinθ=
,即θ=
时,
=
.
(2)∵
=
+
,设点Q(x,y),则
+
=(1+cosθ,sinθ),
=(-x,-y),
∴-x=1+cosθ,-y=sinθ,∴x2+y2=(1+cosθ)2+sin2θ=1,求得cosθ=-
,∴θ=
.
(3)∵a
+
的横坐标为f(θ)=a•cosθ+
,
∴f(θ)+2cos2θ=a•cosθ+
+2cos2θ=2(cosθ+
)2+
-
,
当-
<-1时,f(θ)+2cos2θ的最小值为 2(-1+
)2+
-
;
当-1≤-
≤1时,f(θ)+2cos2θ的最小值为
-
;
当-
>1时,f(θ)+2cos2θ的最小值为 2(1+
)2+
-
.
| AP |
| 1 |
| 2 |
| ||
| 2 |
| OB |
故当cosθ=-
| 1 |
| 2 |
| ||
| 2 |
| 2π |
| 3 |
| AP |
| OB |
(2)∵
| QO |
| OA |
| OB |
| OA |
| OB |
| QO |
∴-x=1+cosθ,-y=sinθ,∴x2+y2=(1+cosθ)2+sin2θ=1,求得cosθ=-
| 1 |
| 2 |
| 2π |
| 3 |
(3)∵a
| OB |
| OP |
| 1 |
| 2 |
∴f(θ)+2cos2θ=a•cosθ+
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| a2 |
| 8 |
当-
| a |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| a2 |
| 8 |
当-1≤-
| a |
| 2 |
| 1 |
| 2 |
| a2 |
| 8 |
当-
| a |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| a2 |
| 8 |
点评:本题考查圆的参数方程,着重考查共线向量坐标间的关系及点在单位圆上,其坐标满足圆的方程的应用,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
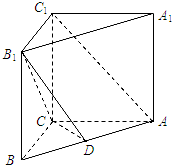 如图,直三棱柱ABC-1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.
如图,直三棱柱ABC-1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.