题目内容
15.设f(x)=x•lnx,g(x)=ax-1,则:(1)若f(x)≥g(x)恒成立,求a的取值范围;
(2)证明:y=$\frac{f(x)}{{x}^{2}}$没有过点P(0,1)的切线;
(3)求证:ln(1+n)>$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n+1}$.
分析 (1)对式子整理得a≤lnx+$\frac{1}{x}$恒成立,只需判断右边式子的最小值即可,利用导函数求最值的方法求解
(2)函数定义域为(0,+∞),点P(0,1)不在定义域内
(3)利用(1)式的结论,整理得恒成立式子ln(x+1)≥$\frac{x}{x+1}$,需利用加减进行叠加,想到令$\frac{1}{n}$=x进行求解.
解答 解:(1)f(x)≥g(x)恒成立
∴x•lnx-ax+1≥0恒成立
∴a≤lnx+$\frac{1}{x}$恒成立
h(x)=lnx+$\frac{1}{x}$
h'(x)=$\frac{x-1}{{x}^{2}}$
x∈(0,1)时,h'(x)<0,h(x)递减
x∈(1,+∞)时,h'(x)>0,h(x)递增
h(x)≥h(1)=1
∴a≤1
(2)y=$\frac{f(x)}{{x}^{2}}$=$\frac{lnx}{x}$
定义域为(0,+∞)
∴P(0,1)没在函数图象上,也没有过点P(0,1)的切线
(3)当a=1时,由(1)得
lnx≥$\frac{x-1}{x}$
∴ln(x+1)≥$\frac{x}{x+1}$
令$\frac{1}{n}$=x
∴ln(n+1)-lnn≥$\frac{1}{n+1}$
ln2-ln1≥$\frac{1}{2}$
ln3-ln2≥$\frac{1}{3}$
…
ln(n+1)-lnn≥$\frac{1}{n+1}$
累加得ln(1+n)>$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n+1}$.
点评 考查了恒成立问题的转换和对结论的分析,探索.

练习册系列答案
相关题目
20.若正方形的棱长为2$\sqrt{2}$,则以该正方形各个面的中心为顶点的凸多面体的体积为( )
| A. | $\frac{\sqrt{2}}{6}$ | B. | $\frac{8\sqrt{2}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2}{3}$ |
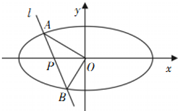 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴一个端点到右焦点的距离为2,直线l过点P(-1,0)且与曲线C交于A,B两点.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴一个端点到右焦点的距离为2,直线l过点P(-1,0)且与曲线C交于A,B两点. 已知矩形ABCD⊥平面BCE,且EB⊥BC,点F是BC的中点,且EB=BC.
已知矩形ABCD⊥平面BCE,且EB⊥BC,点F是BC的中点,且EB=BC.