题目内容
求证:|ax+2|≥|2x+b|恒成立的条件为ab=4且|a|≥2.
证明:由题设可得(ax+2)2≥(2x+b)2,
即(a2-4)x2+(
当a2-4=0时,有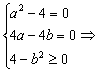 a=b=2或a=b=-2.故命题成立.
a=b=2或a=b=-2.故命题成立.
当a2-4>0时,有![]() 得|a|≥2且(ab-4)2≤0,即|a|≥2且ab=4.故命题成立.
得|a|≥2且(ab-4)2≤0,即|a|≥2且ab=4.故命题成立.
综上知成立的条件为ab=4且|a|≥2.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
题目内容
求证:|ax+2|≥|2x+b|恒成立的条件为ab=4且|a|≥2.
证明:由题设可得(ax+2)2≥(2x+b)2,
即(a2-4)x2+(
当a2-4=0时,有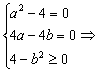 a=b=2或a=b=-2.故命题成立.
a=b=2或a=b=-2.故命题成立.
当a2-4>0时,有![]() 得|a|≥2且(ab-4)2≤0,即|a|≥2且ab=4.故命题成立.
得|a|≥2且(ab-4)2≤0,即|a|≥2且ab=4.故命题成立.
综上知成立的条件为ab=4且|a|≥2.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案