题目内容
一个多面体的直观图(主观图、左视图、俯视图)如图所示,M、N分别为A1B1、B1C1的中点.
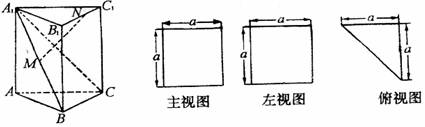
(1)求证:MN∥平面ACC1A1;
(2)求证:MN⊥平面A1BC;
(3)求二面角A―A1B―C的大小.
解:由题意可知,这个几何体是直三棱柱,且AC⊥BC,AC=BC=CC1.
(1)连结AC1,AB1.
由直三棱柱的性质得AA1⊥平面A1B1C1,
所以AA1⊥A1B1,则四边形ABB1A1为矩形.
由矩形性质得AB1过A1B的中点M.
在△AB1C1中,由中位线性质得MN//AC1,
又AC1![]() 平面ACC1A1,MN
平面ACC1A1,MN![]() 平面ACC1A1,
平面ACC1A1,
所以MN//平面ACC1A1
(2)因为BC⊥平面ACC1A1,AC![]() 平面ACC1A1,
平面ACC1A1,
所以BC⊥AC1.
在正方形ACC1A1中,A1C⊥AC1.
又因为BC∩A1C=C,所以AC1⊥平面A1BC.
由MN//AC1,得MN⊥平面A1BC.
(3)由题意CB,CA,CC1两两垂直,故可以C为的点,
CB,CA,CC1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
又AC = BC = CC1 = a,
则![]()
则AB中点E的坐标为![]() ,
,
![]() 为平面AA1B的法向量.
为平面AA1B的法向量.
又AC1⊥平面A1BC,故![]() 为平面A1BC的法向量
为平面A1BC的法向量
设二面角A―A1B―C的大小为θ,
则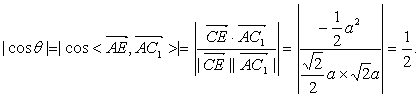
由题意可知,θ为锐角,所以θ= 60°,即二面角A―A1B―C为60°

练习册系列答案
相关题目
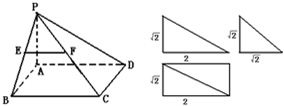 一个多面体的直观图和三视图如图所示,E,F分别为PB,PC中点.
一个多面体的直观图和三视图如图所示,E,F分别为PB,PC中点.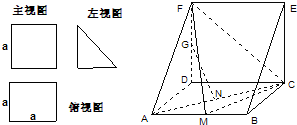
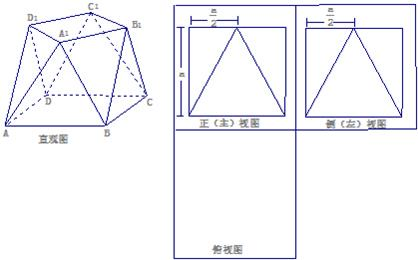 一个多面体的直观图,正(主)视图,侧(左)视图如下所示,其中正(主)视图、侧(左)视图为边长为a的正方形.
一个多面体的直观图,正(主)视图,侧(左)视图如下所示,其中正(主)视图、侧(左)视图为边长为a的正方形.
 一个多面体的直观图及三视图如图所示:(其中M、N、P、Q分别是FC、AF、DC、AD的中点)
一个多面体的直观图及三视图如图所示:(其中M、N、P、Q分别是FC、AF、DC、AD的中点)