题目内容
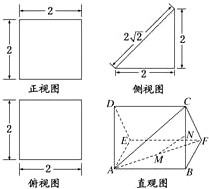
 一个多面体的直观图及三视图如图所示:(其中M、N、P、Q分别是FC、AF、DC、AD的中点)
一个多面体的直观图及三视图如图所示:(其中M、N、P、Q分别是FC、AF、DC、AD的中点)(1)直线DE与直线BF的位置关系是什么、夹角大小为多少?
(2)判断并证明直线MN与直线PQ的位置关系;
(3)求三棱锥D-ABF的体积.
分析:(1)把三视图还原到原图形后可知原几何体是两侧面为正方形且垂直的直三棱柱,所以可知直线DE与直线BF的位置关系且知道夹角;
(2)连接AC后根据三角形中位线定理及平行公理可证明;
(3)三棱锥的地面时等腰直角三角形,高就是AD,则体积可求.
(2)连接AC后根据三角形中位线定理及平行公理可证明;
(3)三棱锥的地面时等腰直角三角形,高就是AD,则体积可求.
解答:解:(1)由三视图分析得到原图形为两个侧面垂直的直三棱柱的平放图形,由图可知直线DE与直线BF的位置关系是异面直线,其夹角为∠BFC,大小为45°;
(2)直线MN与直线PQ的位置关系是平行
证明:连接AC,因为M、N、P、Q分别是FC、AF、DC、AD的中点,所以PQ∥AC,MN∥AC,所以MN∥PQ;
(3)由三视图可知△ABF是边长为2的等腰直角三角形,且三棱锥D-ABF的高为AD=2,
所以VD-ABF=
×S△ABF×AD=
×
×2×2×2=
.
(2)直线MN与直线PQ的位置关系是平行
证明:连接AC,因为M、N、P、Q分别是FC、AF、DC、AD的中点,所以PQ∥AC,MN∥AC,所以MN∥PQ;
(3)由三视图可知△ABF是边长为2的等腰直角三角形,且三棱锥D-ABF的高为AD=2,
所以VD-ABF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
点评:本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 18、一个多面体的直观图及三视图如图所示,M、N分别是AB1、A1C1的中点.
18、一个多面体的直观图及三视图如图所示,M、N分别是AB1、A1C1的中点.
 一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点).
一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点).

