题目内容
已知点A(cosθ,sinθ) (0≤θ≤π)在曲线| 3 |
| 1 |
| 2 |
分析:点A(cosθ,sinθ)代入曲线方程,使用三角公式变形,求得关于某个角的三角函数值,据0≤θ≤π,求出这个角,进而求出θ值.
解答:解:由曲线方程得:
cosθsinθ=
+(sinθ)2,即:
sin2θ=
+
,
即:
sin2θ+
cos2θ=1,sin(2θ+
)=1,
又
≤2θ+
≤2π+
,
∴2θ+
=
,
∴θ=
.
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1-cos2θ |
| 2 |
即:
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
又
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
∴2θ+
| π |
| 6 |
| π |
| 2 |
∴θ=
| π |
| 6 |
点评:本题属于根据三角函数值求角问题,注意灵活使用三角公式.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
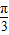 ),sin(α+
),sin(α+ )),点C(1,0).
)),点C(1,0).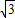 ,求α的值;
,求α的值;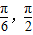 ),求
),求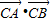 的取值范围.
的取值范围.