题目内容
已知点A(λcosα,λsinα)(λ≠0),B(
,-
),O为坐标原点,
(1)若α=
时,不等式|
|≥2|
|有解,求实数λ的取值范围;
(2)若|
|≥2|
|对任意实数α恒成立,求实数λ的取值范围.
| 1 |
| 2 |
| ||
| 2 |
(1)若α=
| π |
| 6 |
| AB |
| OB |
(2)若|
| AB |
| OB |
(1)|
|≥2|
|有解,即(λcosα-
)2+(λsinα+
)2≥4(2分)
等价于:λ2+1+2λsin(α-
)≥4,代入α=
得:λ2≥3(4分)
即 λ∈(-∞,-
]∪[
,+∞)(6分)
(2)|
|≥2|
|对任意的实数α恒成立,即(λcosα-
)2+(λsinα+
)2≥4对任意的实数α恒成立,即λ2+1+2λsin(α-
)≥4对任意的实数α恒成立 (8分)
所以
或
(12分)
解得:λ≥3或λ≤-3.故所求实数λ的取值范围是(-∞,-3]∪[3,+∞).(14分)
| AB |
| OB |
| 1 |
| 2 |
| ||
| 2 |
等价于:λ2+1+2λsin(α-
| π |
| 6 |
| π |
| 6 |
即 λ∈(-∞,-
| 3 |
| 3 |
(2)|
| AB |
| OB |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
所以
|
|
解得:λ≥3或λ≤-3.故所求实数λ的取值范围是(-∞,-3]∪[3,+∞).(14分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
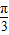 ),sin(α+
),sin(α+ )),点C(1,0).
)),点C(1,0).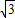 ,求α的值;
,求α的值;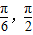 ),求
),求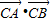 的取值范围.
的取值范围.