题目内容
已知双曲线 的左顶点、右焦点分别为A、F,点B(0,b),若
的左顶点、右焦点分别为A、F,点B(0,b),若 ,则该双曲线离心率e的值为
,则该双曲线离心率e的值为
- A.

- B.

- C.

- D.

B
分析:先求出 和
和 的坐标,由向量的膜的定义,根据
的坐标,由向量的膜的定义,根据 ,建立关于c和a的方程,解方程求得离心率的值.
,建立关于c和a的方程,解方程求得离心率的值.
解答:∵A(-a,0)、F (c,0),B(0,b),
∴ =(-a,-b)+(c,-b)=(c-a,-2b),
=(-a,-b)+(c,-b)=(c-a,-2b), =(-a,-b)-(c,-b)=(-a-c,0),
=(-a,-b)-(c,-b)=(-a-c,0),
∵ ,∴(c-a)2+(-2b)2=(-a-c)2,
,∴(c-a)2+(-2b)2=(-a-c)2,
∴b2=ac,c2-ac-a2=0,e2-e-1=0,再由e>1解得e= ,
,
故选B.
点评:本题考查双曲线的定义和双曲线的标准方程,以及双曲线的简单性质的应用.
分析:先求出
 和
和 的坐标,由向量的膜的定义,根据
的坐标,由向量的膜的定义,根据 ,建立关于c和a的方程,解方程求得离心率的值.
,建立关于c和a的方程,解方程求得离心率的值.解答:∵A(-a,0)、F (c,0),B(0,b),
∴
 =(-a,-b)+(c,-b)=(c-a,-2b),
=(-a,-b)+(c,-b)=(c-a,-2b), =(-a,-b)-(c,-b)=(-a-c,0),
=(-a,-b)-(c,-b)=(-a-c,0),∵
 ,∴(c-a)2+(-2b)2=(-a-c)2,
,∴(c-a)2+(-2b)2=(-a-c)2,∴b2=ac,c2-ac-a2=0,e2-e-1=0,再由e>1解得e=
 ,
,故选B.
点评:本题考查双曲线的定义和双曲线的标准方程,以及双曲线的简单性质的应用.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目

 的左顶点与抛物线
的左顶点与抛物线 的焦点的距离为
的焦点的距离为 ,则双曲线的焦距为
.
,则双曲线的焦距为
. 的左顶点为
的左顶点为 ,右焦点为
,右焦点为 ,
, 为双曲线右支上一点,则
为双曲线右支上一点,则 最小值为 .
最小值为 .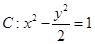 的左顶点为
的左顶点为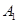 ,右焦点为
,右焦点为 ,
, 为双曲线右支上一点。
为双曲线右支上一点。 的最小值;
的最小值; 为圆
为圆 上动点
上动点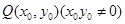 处的切线,且与双曲线
处的切线,且与双曲线 交于不同的两个点
交于不同的两个点 ,证明
,证明 为直角三角形。
为直角三角形。 的左顶点为
的左顶点为 ,右焦点为
,右焦点为 ,
, 为双曲线右支上一点,则
为双曲线右支上一点,则 最小值为 。
最小值为 。