题目内容
 如图,△ABC是正三角形,E、F分别为线段AB、AC上的动点,现将△AEF沿EF折起,使平面AEF⊥平面BCF,设
如图,△ABC是正三角形,E、F分别为线段AB、AC上的动点,现将△AEF沿EF折起,使平面AEF⊥平面BCF,设| AE | AF |
分析:过A作AH垂直EF于H,可证得AH垂直于面BCFE,即得AH垂直于CF,又AE垂直CF,故可证得CF垂直于面AEF,所以CF垂直于EF,由原图可以看出,此时H必与F重合,则∠AFE是个直角,所以∠AEF=30°角,所以AE=2AF,故λ=2,又当AE垂直于底面时显然满足题意,此时有AF=2AE,综合可得答案.
解答: 解:如图过A作AH⊥EF于H,可证得AH⊥面BCFE,即得AH垂直于CF,
解:如图过A作AH⊥EF于H,可证得AH⊥面BCFE,即得AH垂直于CF,
又AE⊥CF,故可证得CF垂⊥AEF,
∴CF⊥EF,由原图可以看出,此时H必与F重合,则∠AFE是个直角,
∴∠AEF=30°,
∴AE=2AF,故λ=2,
又当AE垂直于底面时显然满足题意,
此时有AF=2AE,故此情况下有λ=
综上知应填2或
.
 解:如图过A作AH⊥EF于H,可证得AH⊥面BCFE,即得AH垂直于CF,
解:如图过A作AH⊥EF于H,可证得AH⊥面BCFE,即得AH垂直于CF,又AE⊥CF,故可证得CF垂⊥AEF,
∴CF⊥EF,由原图可以看出,此时H必与F重合,则∠AFE是个直角,
∴∠AEF=30°,
∴AE=2AF,故λ=2,
又当AE垂直于底面时显然满足题意,
此时有AF=2AE,故此情况下有λ=
| 1 |
| 2 |
综上知应填2或
| 1 |
| 2 |
点评:本题考查面面垂直及线面垂直的判定与性质,是一个知识性较强的题,在本题中AE垂直于底面这种情况容易遗漏,是个易失分点.

练习册系列答案
相关题目
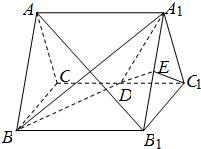 如图,已知正三棱柱ABC-A1B1C1的所有棱长都是2,D、E分别为CC1、A1B1的中点.
如图,已知正三棱柱ABC-A1B1C1的所有棱长都是2,D、E分别为CC1、A1B1的中点. 如图,已知正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)异面直线AC与B1C1所成的角是
如图,已知正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)异面直线AC与B1C1所成的角是 如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是
如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是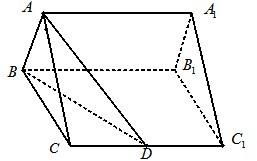 如图,已知正三棱柱ABC-A1B1C1的底面正三角形的边长是2,D是CC1的中点,直线AD与侧面BB1C1C所成的角是45°.
如图,已知正三棱柱ABC-A1B1C1的底面正三角形的边长是2,D是CC1的中点,直线AD与侧面BB1C1C所成的角是45°. 如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,则异面直线AB1和A1C所成的角的余弦值大小是
如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,则异面直线AB1和A1C所成的角的余弦值大小是