题目内容
当实数a,b变化时,直线(2a+b)x+(a+b)y+(a-b)=0与直线m2x+2y-n2=0都过一个定点,记点(m,n)的轨迹为曲线C,P为曲线C上任意一点.若点Q(2,0),则PQ的最大值为 .
考点:直线与圆锥曲线的关系
专题:综合题,圆锥曲线的定义、性质与方程
分析:求出直线(2a+b)x+(a+b)y+(a-b)=0过定点(-2,3),直线m2x+2y-n2=0也过定点(-2,3),将点坐标代入m2x+2y-n2=0,可得-2m2+6-n2=0,即点(m,n)在椭圆
+
=1上,即可求出PQ的最大值.
| m2 |
| 3 |
| n2 |
| 6 |
解答:
解:因为(2a+b)x+(a+b)y+a-b=(2x+y+1)a+(x+y-1)b=0对于任意的a,b都成立,所以2x+y+1=0且x+y-1=0,二者联立,解得x=-2,y=3,即直线(2a+b)x+(a+b)y+(a-b)=0过定点(-2,3).
因此直线m2x+2y-n2=0也过定点(-2,3),将点坐标代入m2x+2y-n2=0,可得-2m2+6-n2=0,即点(m,n)在椭圆
+
=1上.
∵P为曲线C上任意一点,点Q(2,0),
∴PQ的最大值为2+
.
故答案为:2+
.
因此直线m2x+2y-n2=0也过定点(-2,3),将点坐标代入m2x+2y-n2=0,可得-2m2+6-n2=0,即点(m,n)在椭圆
| m2 |
| 3 |
| n2 |
| 6 |
∵P为曲线C上任意一点,点Q(2,0),
∴PQ的最大值为2+
| 3 |
故答案为:2+
| 3 |
点评:本题考查直线与椭圆方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
阅读如图程序框图,下列说法正确的是( )
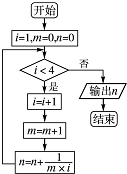

| A、该框图只含有顺序结构、条件结构 |
| B、该框图只含有顺序结构、循环结构 |
| C、该框图只含有条件结构、循环结构 |
| D、该框图包含顺序结构、条件结构、循环结构 |
设复数
=a-bi,则a+b=( )
| 2i-3 |
| 1+i |
| A、1 | B、3 | C、-1 | D、-3 |
已知非空集合A,B,C,若A={y|y=x2,x∈B},B={y|y=
,x∈C},C={y|y=x3,x∈A},则A,B,C的关系为( )
| x |
| A、A=B=C |
| B、A=B?C |
| C、A?B=C |
| D、A?B?C |