题目内容
距离是几何中的基本度量,几何问题和一些实际问题经常涉及距离,如建筑设计中常常需要计算空间两点间的距离试用两点的坐标表示这两点间的距离.
解:(1)在平面直角坐标系中,已知P1(x1,y1),P2(x2,y2),则|P1P2|=
.?
(2)在空间直角坐标系中,?
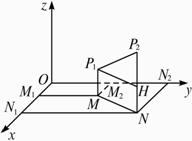
如图,设P1(x1,y1,z1)、P2(x2,y2,z2)是空间中任意两点,且点P1(x1,y1,z1)、P2(x2,y2,z2)在xOy平面上的射影分别为M、N,那么M、N的坐标为M(x1,y1,0)、N(x2,y2,0),在xOy平面上,|MN|=
.?
过点P1作P2N的垂线,垂足为H,则|MP1|=|z1|,|NP2|=|z2|,所以|HP2|=|z2-z1|.?
在Rt△P1HP2中,|P1H|=|MN|=
,根据勾股定理,得?
|P1P2|=
=
.?
因此,空间中点P1(x1,y1,z1),P2(x2,y2,z2)之间的距离?
|P1P2|=
.?
(3)我们来确定P1、P2两点在柱坐标系中的距离公式：?
根据空间点P的直角坐标(x,y,z)与柱坐标(ρ,θ,z)之间的变换公式：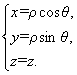
P1(x1,y1,z1),P2(x2,y2,z2),有
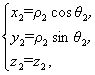可得|P1P2|=
(4)我们来确定P1、P2两点在球坐标系中的距离公式：?
空间点P的直角坐标(x,y,z)与球坐标(r,φ,θ)之间的变换关系为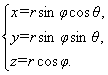
P1(x1,y1,z1),P2(x2,y2,z2),有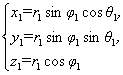
及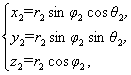
可得|P1P2|=
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，在两个图中三个扇形区域的圆心角分别为
。用这两个转盘进行玩游戏，规则是：同时转动两个转盘待指针停下（当两个转盘中任意一个指针恰好落在分界线时，则这次转动无效，重新开始），记转盘
指针所对的区域数为
，转盘
指针所对的区域为
，
，设
的值为
，每一次游戏得到奖励分为
且
的概率；
次游戏，求他平均可以得到的奖励分
的概率
）
，在两个图中三个扇形区域的圆心角分别为
。用这两个转盘进行玩游戏，规则是：同时转动两个转盘待指针停下（当两个转盘中任意一个指针恰好落在分界线时，则这次转动无效，重新开始），记转盘
指针所对的区域数为
，转盘
指针所对的区域为
，
，设
的值为
，每一次游戏得到奖励分为
且
的概率；
次游戏，求他平均可以得到的奖励分
的概率
）