题目内容
梯形ABCD中,AD∥BC,DC⊥BC,∠B = 60°,AB =BC,E为AB的中点.求证:△ECD为等边三角形.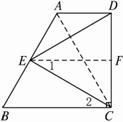
图1-1-21
思路分析:一般在梯形中给出了一腰的中点,常添加的辅助线有:①过这一点作底边的平行线,由平行线等分线段定理推论得另一腰的中点;②可延长DE(或CE)与底边相交,构造全等三角形.

证明:连结AC,过点E作EF∥AD交DC于F.?
∵梯形ABCD,∴AD∥BC.∴AD∥EF∥BC.?
又∵E是AB的中点,∴F是DC的中点
(经过梯形一腰的中点与底平行的直线平分另一腰).?
∵DC⊥BC,∴EF⊥DC.?
∴ED=EC(线段垂直平分线上的点到线段两端点的距离相等).?
∴△EDC为等腰三角形.?
∵AB =BC,∠B =60°,?
∴△ABC是等边三角形.?
∴∠ACB =60°.?
又∵E是AB边中点,?
∴CE平分∠ACB.?
∴∠1=∠2=30°.
∴∠DEF=30°.
∴∠DEC=60°.?
又∵ED=EC,
∴△DEC为等边三角形.

练习册系列答案
相关题目
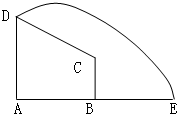 如图,在直角梯形ABCD中,AD∥BC,DA⊥AB,AD=3,AB=4,
如图,在直角梯形ABCD中,AD∥BC,DA⊥AB,AD=3,AB=4,
 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=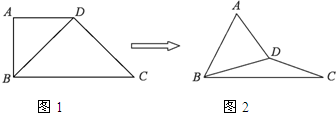

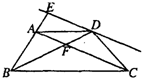 如图,在梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE交BA的延长线于E,AC交BD于F.
如图,在梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE交BA的延长线于E,AC交BD于F.