题目内容
如图(1),四边形ABCD中,E是BC的中点,DB=2,DC=1,BC=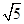 ,AB=AD=
,AB=AD=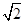 .将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).
.将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).
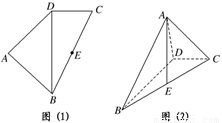
(1)求证:AE⊥平面BDC;
(2)求直线AC与平面ABD所成角的余弦值.
【答案】
(1)见解析 (2)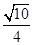
【解析】解:(1)证明:取BD的中点F,连接EF,AF,
则AF=1,EF=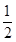 ,∠AFE=60°.
,∠AFE=60°.
由余弦定理知
AE=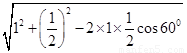 =
=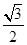 .
.
∵AE2+EF2=AF2,∴AE⊥EF.
∵AB=AD,F为BD中点.∴BD⊥AF.
又BD=2,DC=1,BC=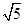 ,
,
∴BD2+DC2=BC2,
即BD⊥CD.
又E为BC中点,EF∥CD,∴BD⊥EF.
又EF∩AF=F,
∴BD⊥平面AEF.又BD⊥AE,
∵BD∩EF=F,
∴AE⊥平面BDC.
(2)以E为原点建立如图所示的空间直角坐标系,则A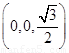 ,
,
C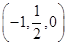 ,
,
B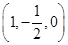 ,
,
D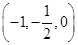 ,
,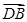 =(2,0,0),
=(2,0,0),
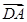 =
=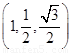 ,
,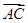 =
=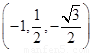 .
.
设平面ABD的法向量为n=(x,y,z),
由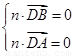 得
得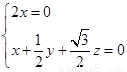
取z=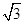 ,
,
则y=-3,又∵n=(0,-3,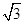 ).
).
∴cos〈n,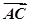 〉=
〉=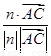 =-
=-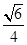 .
.
故直线AC与平面ABD所成角的余弦值为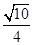 .
.

练习册系列答案
相关题目
 (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知 如图,空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别在BC、CD上,且BG:GC=DH:HC=1:2
如图,空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别在BC、CD上,且BG:GC=DH:HC=1:2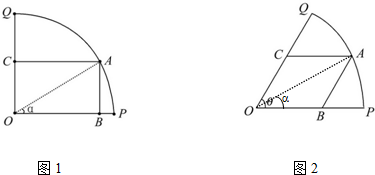 如图1所示,已知OPQ是半径为1,圆心角为θ的扇形,A是扇形弧PQ上的动点,AB∥OQ,OP与AB交于点B,AC∥OP,OQ与AC交于点C.记∠AOP=α.
如图1所示,已知OPQ是半径为1,圆心角为θ的扇形,A是扇形弧PQ上的动点,AB∥OQ,OP与AB交于点B,AC∥OP,OQ与AC交于点C.记∠AOP=α. 如图,平行四边形ABCD中,
如图,平行四边形ABCD中,