题目内容
6.已知数列{an}的前n项和为Sn,a1=1,对于任意n∈N*都有Sn+1-3Sn-1=0.(1)求{an}的通项公式;
(2)若(bn-n)•an=n,求数列{bn}的前n项和Tn.
分析 (1)由对于任意n∈N*都有Sn+1-3Sn-1=0,变形为Sn+1$+\frac{1}{2}$=3(Sn+$\frac{1}{2}$),利用等比数列的通项公式可得Sn,再利用递推关系即可得出.
(2)利用“错位相减法”、等比数列与等差数列的前n项和公式即可得出.
解答 解:(1)∵对于任意n∈N*都有Sn+1-3Sn-1=0,∴Sn+1$+\frac{1}{2}$=3(Sn+$\frac{1}{2}$),
∴数列$\{{S}_{n}+\frac{1}{2}\}$是等比数列,首项为$\frac{3}{2}$,公比为3.
∴Sn+$\frac{1}{2}$=$\frac{3}{2}×{3}^{n-1}$,
∴Sn=$\frac{1}{2}×{3}^{n}$-$\frac{1}{2}$.
∴当n≥2时,an=Sn-Sn-1=$\frac{1}{2}×{3}^{n}$-$\frac{1}{2}$-$(\frac{1}{2}×{3}^{n-1}-\frac{1}{2})$=3n-1.
当n=1时也成立,
∴an=3n-1.
(2)∵(bn-n)•an=n,∴bn=n+$\frac{n}{{3}^{n-1}}$.
设数列$\{\frac{n}{{3}^{n-1}}\}$的前n项和为An,
则An=1+$\frac{2}{3}$+$\frac{3}{{3}^{2}}$+…+$\frac{n}{{3}^{n-1}}$,
$\frac{1}{3}{A}_{n}$=$\frac{1}{3}+\frac{2}{{3}^{2}}$+…+$\frac{n-1}{{3}^{n-1}}$+$\frac{n}{{3}^{n}}$,
∴$\frac{2}{3}{A}_{n}$=$1+\frac{1}{3}+\frac{1}{{3}^{2}}$+…+$\frac{1}{{3}^{n-1}}$-$\frac{n}{{3}^{n}}$=$\frac{1-\frac{1}{{3}^{n}}}{1-\frac{1}{3}}$-$\frac{n}{{3}^{n}}$=$\frac{3}{2}$-$\frac{3+2n}{2×{3}^{n}}$,
∴An=$\frac{9}{4}$-$\frac{3+2n}{4×{3}^{n-1}}$.
∴数列{bn}的前n项和Tn=$\frac{n(n+1)}{2}$+$\frac{9}{4}$-$\frac{3+2n}{4×{3}^{n-1}}$.
点评 本题考查了“错位相减法”、等比数列与等差数列的前n项和公式、递推关系,考查了推理能力与计算能力,属于中档题.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | $\frac{3}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 0 |
| A. | [-15,+∞) | B. | (-∞,2-12$\sqrt{2}$] | C. | (-∞,-16] | D. | (-∞,-15] |
| A. | P(|X1|<1)=P(|X2|<1)=P(|X3|<1) | B. | P(|X1|<1)=P(|X2-1|<1)=P(|X3-1|<1) | ||
| C. | P(|X1|<1)=P(|X2|<1)=P(|X3|<3) | D. | P(|X1|<1)=P(|X2-1|<1)=P(|X3|<3) |
| 速度区间 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) | [100,110) |
| 车辆数 | 1 | 4 | 10 | 15 | 12 | 6 | 2 |
(2)试估计在这段路上,汽车行驶速度的标准差.(注:为了计算方便,速度取每个区间的中点)
| A. | 3 | B. | 3或-3 | C. | 4或-2 | D. | -3 |
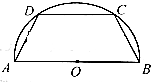 如图,有一块半径为R的半圆形钢板,计划将其剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.
如图,有一块半径为R的半圆形钢板,计划将其剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.