题目内容
(本小题满分12分)
已知函数f (x)=loga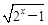 (a>0,a≠1).
(a>0,a≠1).
(1)求函数f (x)的定义域.
(2)求使f (x)>0的x的取值范围.
(1) ;(2)0<a<1时,0<x<1;a>1时,x>1..
;(2)0<a<1时,0<x<1;a>1时,x>1..
解析试题分析:(1)f (x)的定义域是使得 和loga
和loga 有意义的x的取值范围,解得:x>0 5分
有意义的x的取值范围,解得:x>0 5分
(2)根据对数函数的性质,可知,要使f (x)=log >0,
>0,
必须有①0<a<1时,0< <1,解得:0<x<1;
<1,解得:0<x<1;
②a>1时, >1,解得:x>1. ……12分
>1,解得:x>1. ……12分
考点:本题考查函数的定义域;指数函数的单调性;对数函数的单调性。
点评:在解有关指数方程、对数方程时要注意分类讨论。

练习册系列答案
相关题目

 的奇偶性;
的奇偶性; 是奇函数:
是奇函数: 和
和 的值; (2)证明
的值; (2)证明 在区间
在区间 上的单调递减
上的单调递减 且不等式
且不等式 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.  .
. 时,求函数
时,求函数 在
在 上的最大值;
上的最大值; ,若函数
,若函数 有零点,求
有零点,求 的取值范围.
的取值范围. 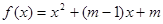 ,
,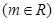
 是偶函数,求
是偶函数,求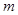 的值。
的值。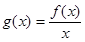 ,
,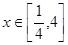 ,求
,求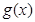 的最小值。
的最小值。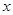 )=
)=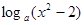 , 若
, 若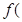 2)=1;
2)=1;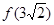 的值;
的值;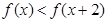
 满足
满足 .
. 的值;
的值;  成立的x的取值范围.
成立的x的取值范围. ,若同时满足下列条件:①
,若同时满足下列条件:① 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[ ]
] ,使
,使 )叫闭函数.
)叫闭函数. 符合条件②的区间[
符合条件②的区间[ 是否为闭函数?并说明理由;
是否为闭函数?并说明理由; 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围.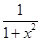 在(-∞,0)上的增减性.
在(-∞,0)上的增减性.