题目内容
(13分) 设函数 .
.
(1)当 时,求函数
时,求函数 在
在 上的最大值;
上的最大值;
(2)记函数 ,若函数
,若函数 有零点,求
有零点,求 的取值范围.
的取值范围.
(1)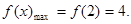 (2)
(2)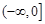 。
。
解析试题分析:(1)化简函数f(x)的解析式,在[1,m]上求函数的最大值.
(2)函数有零点即对应方程有解,得到m的解析式m=h(x),通过导数符号确定h(x)=lnx-x|x-1|的单调性,由h(x)的单调性确定h(x)的取值范围,即得m的取值范围.
(1)当 ,
,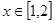 时,
时,
∵函数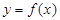 在
在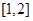 上单调递增 ∴
上单调递增 ∴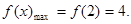
(2)函数 的定义域为
的定义域为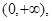
函数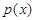 有零点即方程
有零点即方程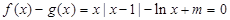 有解
有解
即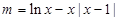 有解
有解
令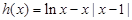 当
当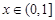 时
时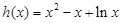
∵
∴函数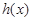 在
在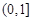 上是增函数,∴
上是增函数,∴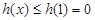
当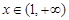 时,
时,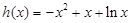
∵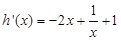
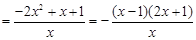
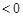
∴函数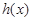 在
在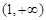 上是减函数,∴
上是减函数,∴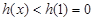
∴方程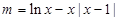 有解时
有解时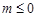
即函数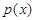 有零点时
有零点时 的取值范围为
的取值范围为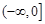 [
[
考点:本题主要是考查用分类讨论的方法求函数最大值,利用导数求函数值域,及化归与转化的思想方法.
点评:解决该试题的关键是根据函数有零点,转化为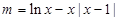 有解,那么借助于分离参数的思想,求解等式右边函数的值域即可。
有解,那么借助于分离参数的思想,求解等式右边函数的值域即可。

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 和
和 组成数对(
组成数对( ,并构成函数
,并构成函数
 ,且
,且 的概率;
的概率; 在区间[
在区间[ 上是增函数的概率.
上是增函数的概率. 为奇函数,
为奇函数,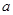 为常数,
为常数, 在区间
在区间 上单调递增;
上单调递增; 上的每一个
上的每一个 值,不等式
值,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里
轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里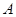 处,如图,现假设:①失事船的移动路径可视为抛物线
处,如图,现假设:①失事船的移动路径可视为抛物线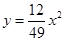 ;②定位后救援船即刻沿直线匀速前往救援;③救援船出发
;②定位后救援船即刻沿直线匀速前往救援;③救援船出发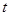 小时后,失事船所在位置的横坐标为
小时后,失事船所在位置的横坐标为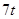

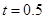 时,写出失事船所在位置
时,写出失事船所在位置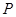 的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向 (若确定方向时涉及到的角为非特殊角,用符号及其满足的条件表示即可)
的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向 (若确定方向时涉及到的角为非特殊角,用符号及其满足的条件表示即可) (0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由.
(0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由. 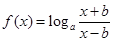
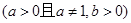 .
. 的定义域;
的定义域;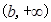 上的单调性.
上的单调性.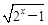 (a>0,a≠1).
(a>0,a≠1).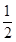 对称,且f′(1)=0.
对称,且f′(1)=0.
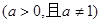
 ;
;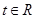 ,不等式
,不等式 恒成立,求
恒成立,求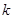 的取值范围。
的取值范围。