题目内容
(本小题满分12分)在平面直角坐标系xOy中,已知定点A(-2,0)、B(2,0),M是动点,且直线MA与直线MB的斜率之积为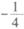 ,设动点M的轨迹为曲线C.
,设动点M的轨迹为曲线C.
(I)求曲线C的方程;
(II)过定点T(-1,0)的动直线 与曲线C交于P,Q两点,若
与曲线C交于P,Q两点,若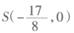 ,证明:
,证明: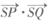 为定值.
为定值.
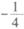 ,设动点M的轨迹为曲线C.
,设动点M的轨迹为曲线C.(I)求曲线C的方程;
(II)过定点T(-1,0)的动直线
 与曲线C交于P,Q两点,若
与曲线C交于P,Q两点,若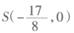 ,证明:
,证明: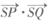 为定值.
为定值.(Ⅰ)设动点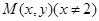 ,则
,则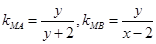 ,……………2分
,……………2分
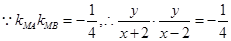 ,
,
即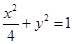 (
(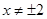 ).…………………4分
).…………………4分
(Ⅱ)当 的斜率不存在时,
的斜率不存在时,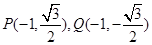 ,
,
若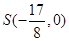 ,
,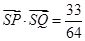 .………………6分
.………………6分
当直线 的斜率存在时,设
的斜率存在时,设 的方程为
的方程为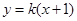 ,
, 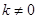 ,联立方程组
,联立方程组
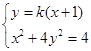 ,消去
,消去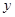 得
得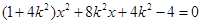 ,
,
设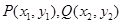 ,则
,则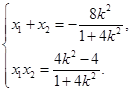 ………………8分
………………8分
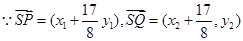 .
.
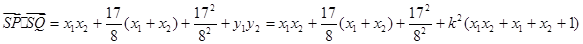
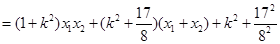 ,
,
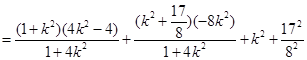 ……………10分
……………10分

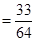 .…………………12分
.…………………12分
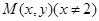 ,则
,则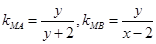 ,……………2分
,……………2分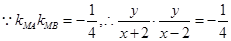 ,
,即
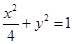 (
(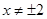 ).…………………4分
).…………………4分(Ⅱ)当
 的斜率不存在时,
的斜率不存在时,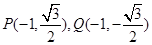 ,
,若
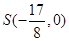 ,
,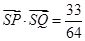 .………………6分
.………………6分当直线
 的斜率存在时,设
的斜率存在时,设 的方程为
的方程为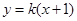 ,
, 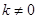 ,联立方程组
,联立方程组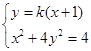 ,消去
,消去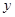 得
得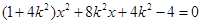 ,
,设
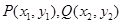 ,则
,则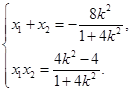 ………………8分
………………8分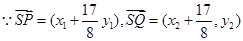 .
.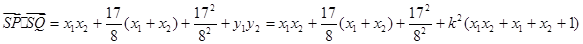
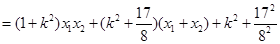 ,
,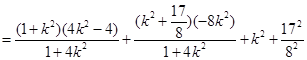 ……………10分
……………10分
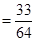 .…………………12分
.…………………12分(I)根据动点满足的几何条件进行坐标化建立方程,然后化简即可得到曲线C的方程。但化简方程时要注意等价转化。
(II)直线方程与曲线C的方程联立消元后,根据韦达定理对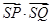 进行坐标化,即可证明。
进行坐标化,即可证明。
(II)直线方程与曲线C的方程联立消元后,根据韦达定理对
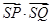 进行坐标化,即可证明。
进行坐标化,即可证明。
练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 中,椭圆
中,椭圆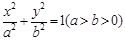 的左、右焦点分别为
的左、右焦点分别为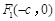 ,
,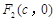 .已知
.已知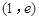 和
和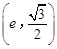 都在椭圆上,其中
都在椭圆上,其中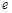 为椭圆的离心率.
为椭圆的离心率.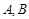 是椭圆上位于
是椭圆上位于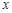 轴上方的两点,且直线
轴上方的两点,且直线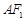 与直线
与直线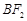 平行,
平行,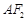 与
与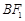 交于点P.
交于点P.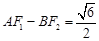 ,求直线
,求直线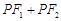 是定值.
是定值.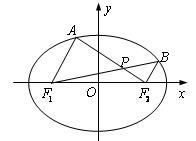
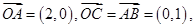 动点
动点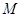 到定直线
到定直线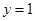 的距离等于
的距离等于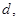 并且满足
并且满足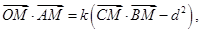 其中
其中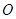 是坐标原点,
是坐标原点,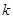 是参数.
是参数.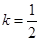 时,求
时,求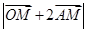 的最大值和最小值;
的最大值和最小值;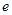 满足
满足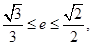 求实数
求实数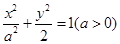 的左、右焦点分别为F1、F2,A是椭圆C上的一点,
的左、右焦点分别为F1、F2,A是椭圆C上的一点,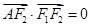 ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为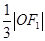 .
.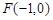 ,交 y 轴于点M,若
,交 y 轴于点M,若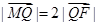 ,求直线l 的斜率.
,求直线l 的斜率.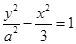 的两个焦点分别为
的两个焦点分别为 、
、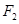 ,离心率为2.
,离心率为2.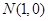 能否作出直线
能否作出直线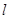 ,使
,使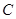 交于
交于 、
、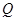 两点,且
两点,且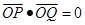 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.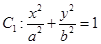 (a>b>0)与双曲线
(a>b>0)与双曲线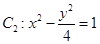 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于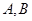 两点.若C1恰好将线段
两点.若C1恰好将线段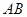 三等分,则
三等分,则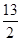
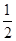
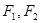 是双曲线
是双曲线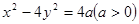 的两个焦点,点
的两个焦点,点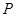 在双曲线上,且满足:
在双曲线上,且满足: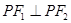 ,
,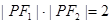 ,则
,则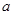 的值为( )
的值为( )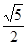
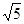
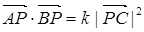 .
.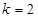 时,求
时,求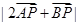 的最大、最小值.
的最大、最小值.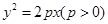 的焦点
的焦点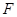 的直线
的直线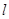 与抛物线在第一象限的交点为
与抛物线在第一象限的交点为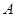 ,与抛物线准线的交点为
,与抛物线准线的交点为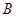 ,点
,点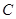 ,若
,若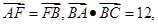 则
则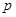 的值为______▲_____________
的值为______▲_____________