题目内容
在正三棱锥P—ABC中,PC垂直于面PAB,PC=2
8![]() π 法一:正三棱锥P—ABC中,PC⊥面PAB,
π 法一:正三棱锥P—ABC中,PC⊥面PAB,
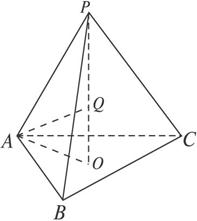
PA、PB![]() 面PAB,∴PA⊥PC,PB⊥PC,∴PA⊥PB.由PA=PC=2
面PAB,∴PA⊥PC,PB⊥PC,∴PA⊥PB.由PA=PC=2![]() ,∴AC=4.
,∴AC=4.
过P作PO⊥面ABC,则外接球的球心Q必在PO上,
连结AQ,设外接球半径为R.
则在Rt△AOQ中,AO=![]() ,
,
PO=![]() =
=![]() =
=![]() =
=![]() .
.
∴OQ=![]() -R,AQ=R.
-R,AQ=R.
由勾股定理:AQ2=OQ2+AO2得R2=(![]() -R)2+(
-R)2+(![]() )2.
)2.
解得R=![]() .∴V球=
.∴V球=![]() R3=8
R3=8![]() π.
π.
法二:∵PA、PB、PC两两垂直,且PA=PB=PC=2![]() ,
,
故过P、A、B、C的球的直径即为边长为2![]() 的正方体的对角线.
的正方体的对角线.
∴2R=2![]() .∴R=
.∴R=![]() .∴V球=
.∴V球=![]() R3=8
R3=8![]() π.
π.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
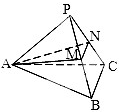 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|