题目内容
15.已知实数x,y满足:x2+2$\sqrt{3}$xy-y2=1,则x2+y2的最小值是$\frac{1}{2}$.分析 由2$\sqrt{3}$xy=y2+1-x2,两边平方,设x2+y2=m,则y2=m-x2,代入可得16x4-4(1+4m)x2+(1+m)2=0,再设x2=t,得到16t2-4(1+4m)t+(1+m)2=0,利用△≥0,解出即可.
解答 解:设x2+y2=m,则y2=m-x2,
∵x2+2$\sqrt{3}$xy-y2=1,
∴2$\sqrt{3}$xy=y2+1-x2,
∴12x2y2=(y2+1-x2)2,
∴12x2(m-x2)=(m+1-2x2)2,
∴16x4-4(1+4m)x2+(1+m)2=0,
设x2=t,
∴16t2-4(1+4m)t+(1+m)2=0
∴△=16(1+4m)2-4×16(m+1)2≥0,解得m≥$\frac{1}{2}$
∴x2+y2的最小值是$\frac{1}{2}$,
故答案为:$\frac{1}{2}$
点评 本题考查了一元二次方程的实数根与判别式的关系、一元二次不等式的解法,属于中档题

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
10.F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的左右焦点,点P在双曲线上,满足$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0,若△PF1F2的内切圆半径与外接圆半径之比为$\frac{\sqrt{3}-1}{2}$,则该双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$+1 | D. | $\sqrt{3}$+1 |
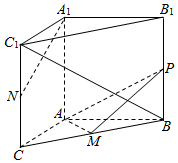 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{3}$.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{3}$.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.