题目内容
设数列{an}中,Sn是它的前n项和,a1=4,nan+1=Sn+n(n+1)对任意n∈N*均成立.(Ⅰ)求证:数列{an}是等差数列;
(Ⅱ)设数列{bn}满足bn+1-bn=an,其中b1=2,求数列{bn}的通项公式;
(Ⅲ)设cn=![]() ,求证:c1+c2+…+cn<1.
,求证:c1+c2+…+cn<1.
解:(Ⅰ)∵nan+1=Sn+n(n+1) ①
∴(n-1)an=Sn-1+(n-1)n(n≥2) ②
①-②整理得,an+1-an=2(n≥2)
又由①,取n=1得a2-a1=2,
∴an+1-an=2(n∈N*)
∴数列{an}是以4为首项,2为公差的等差数列.
(Ⅱ)由(Ⅰ)知an=4+2(n-1)=2(n+1),
∴bn+1-bn=2(n+1),
∴(bn-bn-1)+(bn-1-bn-2)+…+(b3-b2)+(b2-b1)
=2n+2(n-1)+…+2×3+2×2=n2+n-2,
∴bn=n(n+1).
(Ⅲ)由cn=![]() 得,cn=
得,cn=![]() ,
,
∴c1+c2+…+cn=1-![]()
=1-![]() <1.
<1.
证毕.

练习册系列答案
相关题目
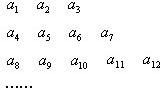 将数列{an}中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表:
将数列{an}中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表: