��Ŀ����
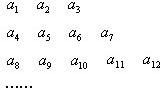 ������{an}�е��������һ����3�����ÿһ�б���һ�ж�һ��Ĺ����ų�����������
������{an}�е��������һ����3�����ÿһ�б���һ�ж�һ��Ĺ����ų������������DZ��еĵ�һ����a1��a4��a8��������������{bn}��
������b8=am����m��ֵ��
������b1=1�������κ�n��N*������bn��0���ң�n+1��bn+12-nbn2+bn+1bn=0��������{bn}��ͨ�ʽ��
�����ڣ����е�����{bn}�����ϱ���ÿһ�е����������ҵ�˳������ɹ���Ϊq��q��0���ĵȱ����У���a66=
| 2 | 5 |
������������������������֪����m=3+4+5+6+7+8+9+1=43��
����������֪
=
�����
=
��
=
������
=
������ʽ��˵�bn=
��
�������ϱ���ÿ�еĹ��ȶ�Ϊq�����е�1������9�й���������bn��ǰ63���a66�ڱ��е�10�е����У��ɴ˿�����ϱ��е�k��k��N*����������ĺ�s��k����
����������֪
| bn+1 |
| bn |
| n |
| n+1 |
| b2 |
| b1 |
| 1 |
| 2 |
| b3 |
| b2 |
| 2 |
| 3 |
| bn |
| bn-1 |
| n-1 |
| n |
| 1 |
| n |
�������ϱ���ÿ�еĹ��ȶ�Ϊq�����е�1������9�й���������bn��ǰ63���a66�ڱ��е�10�е����У��ɴ˿�����ϱ��е�k��k��N*����������ĺ�s��k����
����⣺���������⣬m=3+4+5+6+7+8+9+1=43����4�֣�
�����ɣ�n+1��bn+12-nbn2+bn+1bn=0��bn��0��
��t=
��t��0���ң�n+1��t2+t-n=0��6�֣�
����t+1��[��n+1��t-n]=0��
����
=
��8�֣�
���
=
��
=
������
=
����ʽ��˵�bn=
��10�֣�
�������ϱ���ÿ�еĹ��ȶ�Ϊq����q��0��
��Ϊ3+4+5+��+11=63����12�֣�
���Ա��е�1������9�й���������bn��ǰ63�
��a66�ڱ��е�10�е����У���14�֣�
���a66=b10•q2=
����b10=
������q=2����S(k)=
=
(2k+2-1)��k��N*��16�֣�
�����ɣ�n+1��bn+12-nbn2+bn+1bn=0��bn��0��
��t=
| bn+1 |
| bn |
����t+1��[��n+1��t-n]=0��
����
| bn+1 |
| bn |
| n |
| n+1 |
���
| b2 |
| b1 |
| 1 |
| 2 |
| b3 |
| b2 |
| 2 |
| 3 |
| bn |
| bn-1 |
| n-1 |
| n |
����ʽ��˵�bn=
| 1 |
| n |
�������ϱ���ÿ�еĹ��ȶ�Ϊq����q��0��
��Ϊ3+4+5+��+11=63����12�֣�
���Ա��е�1������9�й���������bn��ǰ63�
��a66�ڱ��е�10�е����У���14�֣�
���a66=b10•q2=
| 2 |
| 5 |
| 1 |
| 10 |
| bk(1-qk+2) |
| 1-q |
| 1 |
| k |
���������⿼�����е����ʺ�Ӧ�ã�����ʱҪ�������⣬��ϸ���

��ϰ��ϵ�д�
�����Ŀ
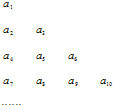 ������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų����±���
������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų����±���
 ������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų������������DZ��е�һ����a1��a2��a4��a7�������ɵ�����Ϊ{bn}��b1=a1=1��SnΪ����{bn}��ǰn��ͣ�������2bn=bnSn-Sn2��n��2��n��N*����
������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų������������DZ��е�һ����a1��a2��a4��a7�������ɵ�����Ϊ{bn}��b1=a1=1��SnΪ����{bn}��ǰn��ͣ�������2bn=bnSn-Sn2��n��2��n��N*���� ������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų����±���
������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų����±���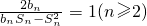 ��
��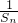 �ɵȲ����У���������{bn}��ͨ�ʽ��
�ɵȲ����У���������{bn}��ͨ�ʽ��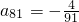 ʱ������q��ֵ��
ʱ������q��ֵ��
 ��bΪ���ڵ���3������������������{cn}���Ƿ������������ɵȱ����У������ڣ�������гɵȱ����е���������������ڣ���˵�����ɣ�
��bΪ���ڵ���3������������������{cn}���Ƿ������������ɵȱ����У������ڣ�������гɵȱ����е���������������ڣ���˵�����ɣ�