题目内容
设直线 是曲线
是曲线
 的一条切线,
的一条切线,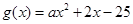 .
.
(1)求切点坐标及 的值;
的值;
(2)当 时,存在
时,存在
 ,求实数
,求实数 的取值范围.
的取值范围.
(1)切点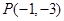 ,
,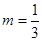 或者切点
或者切点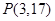 ,
,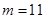 ;(2)
;(2)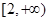 .
.
解析试题分析:(1)先设切点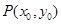 ,然后依题意计算出
,然后依题意计算出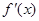 ,由
,由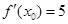 ,计算出切点的横坐标,代入切线的方程,可得切点的纵坐标,最后再将切点的坐标代入曲线C的方程计算得
,计算出切点的横坐标,代入切线的方程,可得切点的纵坐标,最后再将切点的坐标代入曲线C的方程计算得 的值;(2)结合(1)中求出的
的值;(2)结合(1)中求出的 ,确定
,确定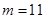 ,设
,设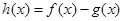 ,然后将存在
,然后将存在 使
使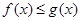 成立问题,转化为
成立问题,转化为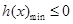 ,进而求出
,进而求出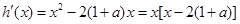 ,分
,分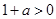 、
、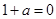 、
、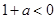 三种情况讨论函数
三种情况讨论函数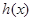 在
在 上的单调性,确定
上的单调性,确定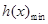 ,相应求解不等式
,相应求解不等式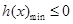 ,即可确定
,即可确定 的取值范围.
的取值范围.
试题解析:(1)设直线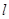 与曲线
与曲线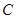 相切于点
相切于点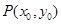
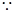
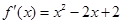 ∴
∴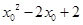
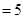 ,解得
,解得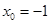 或
或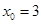
代入直线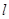 方程,得切点
方程,得切点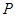 坐标为
坐标为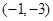 或
或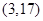
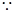 切点
切点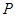 在曲线
在曲线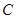 上,∴
上,∴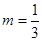 或
或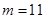
综上可知,切点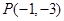 ,
,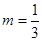 或者切点
或者切点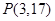 ,
,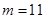 5分
5分
(2)∵ ,∴
,∴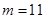 ,设
,设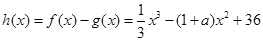 ,若存在
,若存在 使
使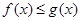 成立,则只要
成立,则只要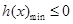 7分
7分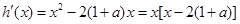
①当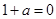 即
即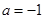 时
时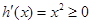 ,
,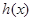 是增函数,
是增函数,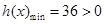 不合题意 8分
不合题意 8分
②若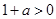 即
即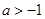
令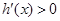 ,得
,得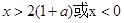 ,∴
,∴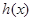 在
在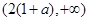 上是增函数
上是增函数
令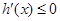 ,解得
,解得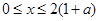 ,∴
,∴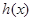 在
在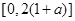 上是减函数
上是减函数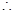
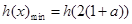 ,
,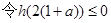 ,解得
,解得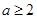 10分
10分
③若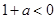 即
即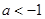 ,
,
令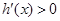 ,解得
,解得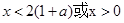
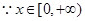 ,∴
,∴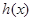 在
在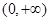 上是增函数
上是增函数
∴
练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围; +
+ +…+
+…+ >ln(n+1)都成立.
>ln(n+1)都成立. (f′(x)是f(x)的导函数)在区间(t,3)上总不是单调函数,求m的取值范围;
(f′(x)是f(x)的导函数)在区间(t,3)上总不是单调函数,求m的取值范围; ×…×
×…× <
< (n≥2,n∈N*)
(n≥2,n∈N*)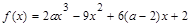 ,
, .
. 在
在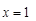 处取得极值,求实数
处取得极值,求实数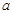 的值;
的值;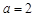 ,求函数
,求函数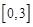 上的最大值和最小值.
上的最大值和最小值. .
. .的单调区间;
.的单调区间; 的极值.
的极值.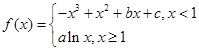 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点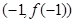 处的切线斜率为
处的切线斜率为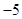 .
.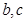 的值;
的值; 在区间
在区间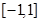 上的最小值;
上的最小值;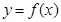 的图像上存在两点
的图像上存在两点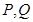 ,使得对于任意给定的正实数
,使得对于任意给定的正实数 都满足
都满足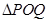 是以
是以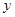 轴上,求点
轴上,求点 的横坐标的取值范围.
的横坐标的取值范围. 为函数
为函数 图象上一点,
图象上一点, 为坐标原点,记直线
为坐标原点,记直线 的斜率
的斜率 .
. 在区间
在区间
 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围; ,
, ,有
,有 ,求实数
,求实数 的取值范围.
的取值范围.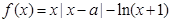 .
. 时,求函数
时,求函数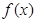 的单调区间;
的单调区间;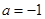 时,若
时,若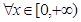 ,
,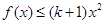 恒成立,求实数
恒成立,求实数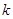 的最小值;
的最小值;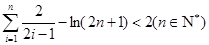 .
.