题目内容
已知函数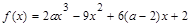 ,
,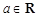 .
.
(1)若函数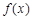 在
在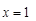 处取得极值,求实数
处取得极值,求实数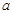 的值;
的值;
(2)若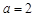 ,求函数
,求函数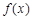 在区间
在区间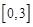 上的最大值和最小值.
上的最大值和最小值.
(1)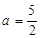 (2)最小值
(2)最小值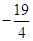 ,最大值29
,最大值29
解析试题分析:(1)先求导,因为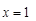 是函数
是函数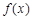 的极值点,则
的极值点,则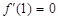 ,即可求实数
,即可求实数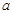 的值。(2)先求导再令导数等于0,导论导数的正负得函数的增减区间,根据函数的增减性可求其最值。
的值。(2)先求导再令导数等于0,导论导数的正负得函数的增减区间,根据函数的增减性可求其最值。
试题解析:解答:(1)∵函数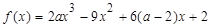 ,
,
∴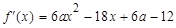 . 2分
. 2分
∵函数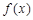 在
在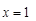 处取得极值,∴
处取得极值,∴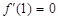 ,
,
∴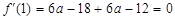 ,∴实数
,∴实数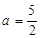 . 4分
. 4分
经检验,当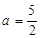 时,
时,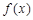 取得极小值,故
取得极小值,故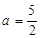 . 6分
. 6分
(2)当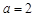 时,
时,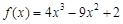 .
.
∵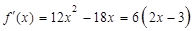 ,∴
,∴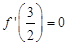 . 8分
. 8分
∵在区间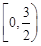 上,
上,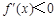 ;在区间
;在区间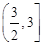 上,
上, ,
,
∴在区间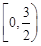 上,函数
上,函数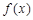 单调递减;在区间
单调递减;在区间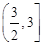 上,函数
上,函数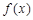 单调递增.10分
单调递增.10分
∴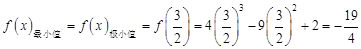 . 11分
. 11分
∵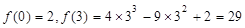 ,∴
,∴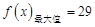 . 12分
. 12分
考点:1导数;2用导数研究函数的单调性。

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
 .
.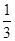 ax3-
ax3- x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.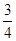 x2-bx+
x2-bx+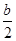 -
- +x(a≠0),
+x(a≠0),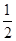 ,求证:当x∈(0,+∞)时,f(x)>1;
,求证:当x∈(0,+∞)时,f(x)>1; <e4(n∈N*)..
<e4(n∈N*).. 是曲线
是曲线
 的一条切线,
的一条切线,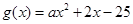 .
. 的值;
的值; 时,存在
时,存在
 ,求实数
,求实数 的取值范围.
的取值范围.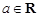 ,函数
,函数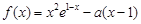 .
.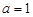 时,求
时,求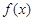 在
在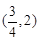 内的极大值;
内的极大值;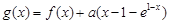 ,当
,当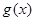 有两个极值点
有两个极值点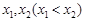 时,总有
时,总有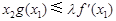 ,求实数
,求实数 的值.(其中
的值.(其中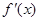 是
是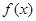 的导函数.)
的导函数.)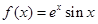 函数.
函数.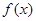 单调递增区间;
单调递增区间;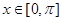 时,求函数
时,求函数 。
。 的极值点;
的极值点; 时,若方程
时,若方程 在
在 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围; 时,
时, 。
。