题目内容
（本题满分10分）选修4—4:坐标系与参数方程.
坐标系与参数方程在直角坐标系xOy中,圆C的参数方程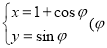
为参数）.以O为极点,x轴的非负半轴为极轴建立极坐标系.
（Ⅰ）求圆C的极坐标方程；
（Ⅱ）射线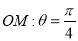
与圆C的交点为O、P两点，求P点的极坐标.
（Ⅰ） 
；（Ⅱ） 
【解析】
试题分析：（Ⅰ）圆C的普通方程是
，利用
，可得圆C的极坐标方程是；（Ⅱ）把
代入得
所以P点的极坐标为
试题解析：（Ⅰ）圆C的普通方程是，又
所以圆C的极坐标方程是 5分
（Ⅱ）因为射线
的普通方程为
联立方程组
消去
并整理得
解得
或
，所以P点的坐标为
所以P点的极坐标为 10分
解法2：把代入得
所以P点的极坐标为 10分
考点：参数方程
考点分析： 考点1：坐标系与参数方程 考点2：参数方程 试题属性- 题型：
- 难度：
- 考核：
- 年级：
练习册系列答案
名校课堂系列答案
相关题目
的正方体的顶点都在球面上,则该球的表面积等于（ ）
B．
C．
D．
上横坐标是2的点
到抛物线焦点距离是3，则
（ ）
的左，右焦点分别为
，点
在双曲线上，且满足
，则△
的面积为（ ）
B. 
C. 
D. 
的不等式组
，表示的平面区域是直角三角形区域，则正数
的值为（ ）
四所中学的学生当中随机抽取50名学生参加问卷调查，已知
名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率；
两所中学的学生当中随机抽取两名学生,用
表示抽得
中学的学生人数,求
的分布列及期望值.
的大小为
，平面
上的曲线
在平面
上的正射影为曲线
，
在直角坐标系
下的方程
，则曲线
的离心率（ ）
B.
C.
D.
，
，则集合
等于（ ）
B. 
C. 
D. 