题目内容
(12分)某高校在2012年的自主招生考试中随机抽取了100名学生的笔试成绩,按成绩分组:第一组[160,165),第二组[165,170),第三组[170,175),第四组[175,180),第五组[180,185)得到的频率分布直方图如图所示.
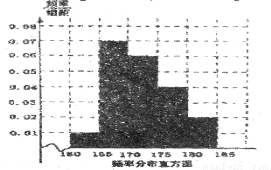
(1)求第三、四、五组的频率;
(2)为了以选拔出最优秀的学生,学校决定在笔试成绩高的第三、四、五组中用分层抽样抽取6名学生进入第二轮面试,求第三、四、五组每组各抽取多少名学生进入第二轮面试.
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第四组至少有一名学生被甲考官面试的概率.
(1)0.3,0.2,0.1;(2)3人,2人,1人;(3)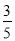
【解析】
试题分析:(1)如频率分布直方图可知,小正方形的面积为频率,根据所给的数据可得到第三、四、五组的频率.
(2)根据频率分布直方图可求出第三、四、五组的人数,即可得每组占这三组人数和的百分比,由分层抽样抽的实验方法,即可得每组所取得人数.
(3)由6名学生中抽取两名学生共有15种情况,由于第四组有两名学生.至少有一名被抽到的情况包括两种情况,只有一个被抽到和两个都被抽到.共9种情况.即可得结论.
试题解析:(1)由题设可知,第三组的频率为0.06×5=0.3第四组的频率为0.04×5=0.2第五组的频率为0.02×5=0.1
(2)第三组的人数为0.3×100=30 第四组的人数为0.2×100=20第五组的人数为0.1×100=10因为第三、四、五组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组抽到的人数分别为:第三组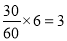 第四组
第四组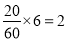 第五组
第五组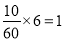 ,所以第三、四、五组分别抽取3人,2人,1人.
,所以第三、四、五组分别抽取3人,2人,1人.
(3)设第三组的3位同学为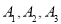 ,第四组的2为同学为
,第四组的2为同学为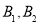 ,第五组的1为同学为C1,则从6为同学中抽2位同学有:
,第五组的1为同学为C1,则从6为同学中抽2位同学有: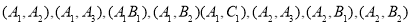
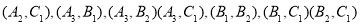 共15种可能其中第四组的2为同学
共15种可能其中第四组的2为同学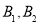 中至少1为同学入选有
中至少1为同学入选有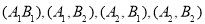 ,
,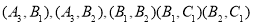 共9种可能。
共9种可能。
所以第四组至少有1位同学被甲考官面试的概率为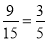 .
.
考点:1.统计概率问题.2.分层抽样.3.列举法.
考点分析: 考点1:古典概率 试题属性- 题型:
- 难度:
- 考核:
- 年级:

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 :
:  ,求曲线
,求曲线 在
在 轴上的所截的线段的长度为1的充要条件,证明你的结论.
轴上的所截的线段的长度为1的充要条件,证明你的结论.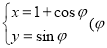 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.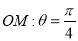 与圆C的交点为O、P两点,求P点的极坐标.
与圆C的交点为O、P两点,求P点的极坐标. 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的主视图时,以
中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的主视图时,以 平面为投影面,则得到主视图可以为( )
平面为投影面,则得到主视图可以为( )
 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为 .
. ).
). 的根
的根 ,则k=_____.
,则k=_____. ,
,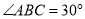 , AD是边BC上的高,则
, AD是边BC上的高,则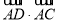 的值等于( )
的值等于( )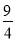 C.4 D.
C.4 D.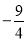
 ,
, ,
, 的夹角为60°,则
的夹角为60°,则 _____.
_____. ,点
,点 ,以线段AB为直径的圆内切于圆
,以线段AB为直径的圆内切于圆 ,记点B的轨迹为
,记点B的轨迹为 .
.
 的方程;
的方程;