在△ABC中.∠A=60°.∠B=45°.BC=$\sqrt{3}$.那么AC等于( )A．$\sqrt{6}$B．$\sqrt{2}$C．1D．$\frac{{\sqrt{2}}}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

7．在△ABC中，∠A=60°，∠B=45°，BC=$\sqrt{3}$，那么AC等于（　　）

A．

$\sqrt{6}$

B．

$\sqrt{2}$

C．

D．

$\frac{{\sqrt{2}}}{2}$

分析由正弦定理得$\frac{BC}{sinA}=\frac{AC}{sinB}$，可得AC．

解答解：在△ABC中，由正弦定理得$\frac{BC}{sinA}=\frac{AC}{sinB}$
⇒$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=$\frac{AC}{\frac{\sqrt{2}}{2}}$⇒AC=$\sqrt{2}$．
故选：B

点评本题考查了正弦定理，属于基础题．

练习册系列答案

重点中学与你有约系列答案

绿色成长互动空间决胜中考模拟卷系列答案

18．设p是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{9}$=1上一点，双曲线的一条渐近线方程为3x-2y=0，F₁，F₂分别是双曲线的左、右焦点，若|PF₁|=5，则|PF₂|=（　　）

15．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）右焦点为F，右顶点为A，一条渐近线方程为y=2$\sqrt{2}$x，且|AF|=2，则该双曲线的实轴长为（　　）

2．

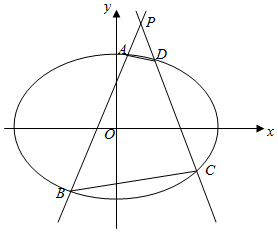如图，在平面直角坐标系xOy中，已知椭圆Γ：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别为F₁（-$\sqrt{3}$，0），F₂（$\sqrt{3}$，0），且椭圆Γ的上顶点到直线$\sqrt{3}$x+y+1=0的距离等于1．
（1）求椭圆Γ的标准方程；
（2）过点P（1，2）作两条倾斜角互补的两直线l₁，l₂分别交椭圆Γ于A，B，C，D四点，求k_AC+k_BD的值．

12．函数f（x）=log₂sin（$\frac{π}{4}$-$\frac{π}{4}$x）的单调增区间为（　　）

19．若等比数列{a_n}的前n项和S_n=3ⁿ-1，则其公比为（　　）

16．已知点P，Q为圆C：x²+y²=25上的任意两点，且|PQ|≤8，若PQ的中心点组成的区域为M，在圆C内任取一点，则该点落在区域M内的概率为$\frac{16}{25}$．

6．求P（x，y）是直角坐标平面xOy上的一个动点，点P到直线x=8的距离等于它到点M（2，0）的距离．
（1）求动点P的轨迹C₁的方程，并指出该轨迹为何种圆锥曲线；
（2）求曲线C₁关于直线x=8的对称曲线C₂的方程及曲线C₂的焦点坐标．

试题分类