题目内容
已知函数 .
.(1)判断f(x)的奇偶性并给出证明;
(2)若f(x)=2x•k有两个不同的实数根,求k的取值范围.
【答案】分析:(1)要判定函数的奇偶性,只有按照定义进行,即先求函数的定义域,再判定f(-x)与f(x)的关系.
(2)若方程有两个不等的实根,则说明等号左右的两个函数有两个不同的交点,可以转化为一元二次方程用△来处理.
解答:解:函数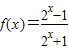 为R上的奇函数.
为R上的奇函数.
证明:由题得函数的定义域为R,关于原点对称.
又f(-x)=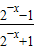 =
=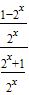 =
=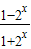 =-f(x)
=-f(x)
故函数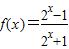 在R上为奇函数.
在R上为奇函数.
(2)由f(x)=2x•k 整理得: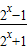 =
=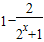 =2x•k
=2x•k
设2x=t,则t>0,上式可化为1-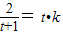 ,
,
化简得kt2+(k-1)t+1=0,由题可知该式有两个不等的实根.
所以,判别式△=(k-1)2-4k>0
解得,k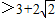 ,或
,或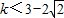 .
.
故k的取值范围为 k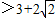 ,或
,或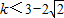 .
.
点评:1、定义域关于原点对称是函数具有奇偶性的必要(但不充分)条件.
2、判定函数奇偶性常见步骤:
①判定其定义域是否关于原点对称,
②判定f(x)与f(-x)的关系.
(2)若方程有两个不等的实根,则说明等号左右的两个函数有两个不同的交点,可以转化为一元二次方程用△来处理.
解答:解:函数
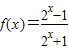 为R上的奇函数.
为R上的奇函数.证明:由题得函数的定义域为R,关于原点对称.
又f(-x)=
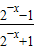 =
=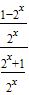 =
=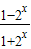 =-f(x)
=-f(x)故函数
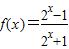 在R上为奇函数.
在R上为奇函数.(2)由f(x)=2x•k 整理得:
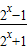 =
=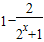 =2x•k
=2x•k设2x=t,则t>0,上式可化为1-
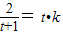 ,
,化简得kt2+(k-1)t+1=0,由题可知该式有两个不等的实根.
所以,判别式△=(k-1)2-4k>0
解得,k
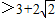 ,或
,或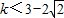 .
.故k的取值范围为 k
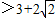 ,或
,或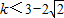 .
.点评:1、定义域关于原点对称是函数具有奇偶性的必要(但不充分)条件.
2、判定函数奇偶性常见步骤:
①判定其定义域是否关于原点对称,
②判定f(x)与f(-x)的关系.

练习册系列答案
相关题目

 ,
, 上的单调性;
上的单调性; .
. ,求a,b的值.
,求a,b的值. .
. 的奇偶性;(4分)
的奇偶性;(4分) 的方程
的方程 有两解,求实数
有两解,求实数 的取值范围;(6分)
的取值范围;(6分) ,记
,记 ,试求函数
,试求函数 在区间
在区间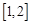 上的最大值.(10分)
上的最大值.(10分) .
. ,
, 的奇偶性;(2)求证:方程
的奇偶性;(2)求证:方程 至少有一根在区间
至少有一根在区间