题目内容
(本小题12分)已知函数
 ,
,
(1)判断函数在区间 上的单调性;
上的单调性;
(2)求函数在区间是区间[2,6]上的最大值和最小值.
【答案】
(1)函数
 是区间
是区间 上的减函数;(2)
上的减函数;(2) ,
,
【解析】
试题分析:(1)设 是区间
是区间 上的任意两个实数,且
上的任意两个实数,且 ,则
,则

 -
- =
= =
= .
.
由 得
得 ,
, ,
,
于是 ,即
,即 .
.
所以函数
 是区间
是区间 上的减函数.
……6分
上的减函数.
……6分
(2)由(1)知函数函数
 在区间的两个端点上分别取得最大值与最小值,
在区间的两个端点上分别取得最大值与最小值,
即当 时,
时, ;当
;当 时,
时, . ……12分
. ……12分
考点:本小题主要考查利用定义判断函数的单调性和利用函数的单调性求函数的最值,考查学生对定义的掌握和利用能力以及数形结合思想的应用.
点评:利用单调性的定义判断或证明函数的单调性时,要把结果划到最简,尽量不要用已知函数的单调性判断未知函数的单调性.

练习册系列答案
相关题目
 中,
中, 。
。 中,
中, ,求数列
,求数列 项和
项和 .
. 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程 ;
; 过
过 且与圆C相切,求直线
且与圆C相切,求直线 ,使直线
,使直线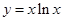
 处的切线方程。
处的切线方程。