题目内容
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,其导函数为
上的偶函数,其导函数为![]() ,且当
,且当![]() 时,
时,![]() ,则不等式
,则不等式![]() 的解集为_______.
的解集为_______.
【答案】![]()
【解析】
构造函数F(x)=x2f(x),结合题意,得出F(x)在(-∞,0)是增函数,原不等式等价为![]() ,结合函数的单调性和奇偶性求解即可.
,结合函数的单调性和奇偶性求解即可.
已知2f(x)+xf′(x)<0,x<0;则2xf(x)+x2f′(x)>0,
即[x2f(x)]′>0;令F(x)=x2f(x),
则当x<0时,![]() >0,即F(x)在(-∞,0)上是增函数,
>0,即F(x)在(-∞,0)上是增函数,
∵F(x-2018)=(x-2018)2f(x-2018),F(-1)=f(-1),
∴不等式等价为F(x-2018)-F(-1)<0,
∵偶函数f(x)是定义在R上的可导函数,f(-x)=f(x),∴F(-x)=F(x),
∵F(x)在(-∞,0)是增函数,∴F(x)在(0,+∞)是减函数,
由F(2018-x)=F(x-2018)<F(-1)=F(1)得,|x-2018|>1,
解得x>2019或x<2017.
故填:{x|x<2017或x>2019}.

 阅读快车系列答案
阅读快车系列答案【题目】某媒体为调查喜爱娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
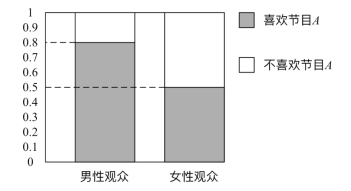
根据该等高条形图,完成下列2×2列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目A与观众性别有关?
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 | 60 |
附: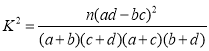
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某企业生产某种产品,为了提高生产效益,通过引进先进的生产技术和管理方式进行改革,并对改革后该产品的产量x(万件)与原材料消耗量y(吨)及100件产品中合格品与不合格品数量作了记录,以便和改革前作对照分析,以下是记录的数据:
表一:改革后产品的产量和相应的原材料消耗量
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
表二:改革前后定期抽查产品的合格数与不合格数
合格品的数量 | 不合格品的数量 | 合计 | |
改革前 | 90 | 10 | 100 |
改革后 | 85 | 15 | 100 |
合计 | 175 | 25 | 200 |
(1)请根据表一提供数据,用最小二乘法求出y关于x的线性回归方程![]() .
.
(2)已知改革前生产7万件产品需要6.5吨原材料,根据回归方程预测生产7万件产品能够节省多少原材料?
(3)请根据表二提供的数据,判断是否有90%的把握认为“改革前后生产的产品的合格率有差异”?






