题目内容
设f(x)=cos2x+sinx,则下列结论正确的一个是
- A.f(x)的最大值为2,最小值为0
- B.f(x)的最大值为
 ,最小值为-1
,最小值为-1 - C.f(x)的最大值为
 ,最小值为-1
,最小值为-1 - D.f(x)的最大值为
 ,最小值为0
,最小值为0
B
分析:利用sin2x+cos2x=1可将f(x)=cos2x+sinx转化为关于sinx的一元二次方程,利用正弦函数与二次函数的性质即可求得答案.
解答:∵f(x)=cos2x+sinx=1-sin2x+sinx=- +
+ ,
,
∵-1≤sinx≤1,
∴当sinx= 时,f(x)max=
时,f(x)max= ,
,
当sinx=-1时,f(x)min=-1,
故选B.
点评:本题考查同角三角函数间的基本关系,考查正弦函数与二次函数的性质,考查转化思想与方程思想,属于中当题.
分析:利用sin2x+cos2x=1可将f(x)=cos2x+sinx转化为关于sinx的一元二次方程,利用正弦函数与二次函数的性质即可求得答案.
解答:∵f(x)=cos2x+sinx=1-sin2x+sinx=-
 +
+ ,
,∵-1≤sinx≤1,
∴当sinx=
 时,f(x)max=
时,f(x)max= ,
,当sinx=-1时,f(x)min=-1,
故选B.
点评:本题考查同角三角函数间的基本关系,考查正弦函数与二次函数的性质,考查转化思想与方程思想,属于中当题.

练习册系列答案
相关题目
 sinωxcosωx
sinωxcosωx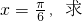 ω的值.
ω的值. sinωxcosωx
sinωxcosωx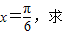 ω的值.
ω的值.